Portfolio-Theorie, Modellbeurteilung

1. Portfolio-Theorie i.e.S. (bis zur Ermittlung der Effizienzkurve):
a) Positive Aspekte: In der vor allem auf Markowitz zurückgehenden Portfolio-Theorie wurde erstmals neben der Rendite- auch die Risikodimension von Kapitalanlagen in quantitativer Form und vor allem simultan mit der Renditedimension erörtert; zuvor war ein sukzessives Vorgehen üblich, nach dem Risikozuschläge im Kalkulationszinsfuß angesetzt wurden und die anschließende Optimierung nach Renditekriterien erfolgte. Weiterhin wurde anstelle der isolierten Betrachtung von Einzelwerten gemäß der traditionellen Aktienanalyse die Zusammenstellung ganzer Portfolios in den Mittelpunkt der Aufmerksamkeit gerückt. Dabei gelang erstmals die operationale Handhabung des (schon früher bekannten) Diversifikationseffektes, indem die zentrale Bedeutung der Korrelation der Renditen der einzelnen Anlagen herausgearbeitet und anhand statistischer Maßgrößen (Kovarianzen, Korrelationskoeffizienten) quantifiziert werden konnte. Nicht zuletzt konnte eine fundierte Erklärung des empirisch beobachtbaren Diversifikationsverhaltens von Anlegern gewonnen und so auch ein wesentlicher Beitrag zur Begründung des Investmentgeschäfts geleistet werden.

b) Kritische Aspekte: Die Messung des Risikos im Grundmodell anhand der Varianz oder Standardabweichung der Renditen war bereits von Markowitz selbst kritisch gesehen und mit dem Hinweis auf eine vereinfachte Anwendbarkeit gerechtfertigt worden. Sie fußt letztlich auf der Annahme einer Normalverteilung der Renditen (vgl. genauer Mean-Variance-Approach), die sich als empirisch kaum haltbar erwiesen hat: So sind u.a. empirisch gemessene Aktienrenditen oftmals (längerfristig) linksschief, also asymmetrisch verteilt. Das bedeutet, dass kleine Gewinne zwar häufiger auftreten als kleine Verluste, aber umgekehrt große Verluste auch häufiger als große Gewinne; es wird davon ausgegangen, dass diese Konstellation dem repräsentativen Anleger nicht recht ist, d.h. er "mag Schiefe", die als 3. Moment der Wahrscheinlichkeitsverteilung (Verteilungsfunktion) der Renditen im umgekehrten Fall der Rechtsschiefe ein positives Vorzeichen trägt. Weiterhin zeigen gemessene Renditen (kürzerfristig) sog. "fat tails" ("schwere Flanken", Leptokurtosis), d.h. es kommt zu im Vergleich zur Normalverteilung überdurchschnittlich vielen "Renditeausreißern" nach unten wie nach oben, denen eine "peakedness around the mean" (überdurchschnittlich viele kleine Kurs-, genauer: Renditebewegungen) gegenübersteht. Es wird davon ausgegangen, dass auch dieses Bild dem repräsentativen Anleger nicht gefällt, d.h. "er mag keine Wölbung (Kurtosis)", die als 4. Moment der Wahrscheinlichkeitsverteilung der Renditen einen Wert von >3 aufweist; dieser Wert ergibt sich daraus, dass bereits die Nomalverteilung mit einer Wölbung von +3 aus statistischer Perspektive als recht "spitzgipfelig" angesehen werden kann. Es ist jedoch zu beachten, dass sich derartige Abweichungen von der Normalverteilung dann tendenziell ausgleichen, wenn die Anleger zumindest annähernd sog. "wohldiversifizierte" Portefeuilles halten, in denen über das Gesamtportfolio gesehen aus statistischen Gründen (sog. "Zentraler Grenzwertsatz") die Normalverteilungsannahme zulässig erscheint. Auch wenn die theoretisch-statistischen Voraussetzungen hierfür nicht ohne Weiteres als gegeben angenommen werden können, hat sich die Risikomessung von Markowitz als hinreichend tragfähig und vor allem als fruchtbar erwiesen. Bei der Einbeziehung von Optionspositionen (und Wertpapieren mit Optionselementen) ist das Grundmodell der Portfolio-Theorie infolge der ausgeprägten Rechtsschiefe (bei Long-Positionen: keine großen Verluste) bzw. Linksschiefe (bei Short-Positionen: keine großen Gewinne) der entsprechenden Renditeverteilungen allerdings nicht anwendbar.

Neben diesen konzeptionellen Problemen ergeben sich Schwierigkeiten bei der praktischen Modellanwendung vor allem hinsichtlich der Ermittlung der erforderlichen Inputdaten (erwartete Renditen, Varianzen/Standardabweichungen, Kovarianzen/Korrelationskoeffizienten), und zwar sowohl in quantitativer als auch in qualitativer Hinsicht: Zunächst stand das Problem im Vordergrund, dass die enorme Menge zu schätzender Daten sowohl aus datenverarbeitungs- als auch aus verfahrenstechnischer Sicht die praktische Anwendbarkeit stark beeinträchtigt hat; vgl. Index-Modell). In der jüngeren Zeit gilt der inhaltlichen Problematik einer "brauchbaren" Prognose für die Modellparameter über den jeweiligen Anlagehorizont die größte Aufmerksamkeit (Asset Allocation, Grundprinzipien): In Anbetracht der beobachtbaren Instabilität der Parameterwerte im Zeitablauf verbietet sich eine schlichte Fortschreibung historisch gewonnener Daten bzw. eine Investition in lediglich in der Vergangenheit effiziente Portefeuilles. Dies gilt weniger für die Kovarianzen/Korrelationskoeffizienten (bzw. Beta-Faktoren), eher schon für die Varianzen/Standardabweichungen (historische Volatilität), aber vor allem für die einzelnen Renditen, die sich – außer für sehr langfristige Betrachtungen – der Möglichkeit einer Fortschreibung aus der Vergangenheit weitestgehend entziehen. Hinzu kommt, dass die Modellergebnisse (und damit letztlich die Portfoliozusammensetzung) extrem sensitiv gerade auf bereits geringe Veränderungen bei den Renditeprognosen und damit auf dahingehende Prognosefehler reagieren. Zur Einordnung dieser Problemlage ist allerdings festzuhalten, dass die Bewältigung der Prognoseaufgabe zum einen nicht Bestandteil der Portfolio-Theorie ist, sondern in das Arbeitsgebiet der Wertpapieranalyse fällt, die der Portfolio-Theorie vorgeschaltet ist und ihr in arbeitsteiliger Form zuarbeitet; zum anderen wird in der Portfolio-Theorie ja die große Bedeutung der Kovarianzen/Korrelationskoeffizienten herausgestellt, die sich nun aber gerade als besser prognostizierbar erwiesen haben. Schließlich kann das Grundmodell der Portfolio-Theorie als statisches Modell keinerlei Anhaltspunkte für die Lösung des in der Praxis so wichtigen Timing-Problems, d.h. der Wahl der richtigen Kauf- und Verkaufszeitpunkte, liefern.

2. Portfolio-Theorie i.w.S. (bis zur Zusammenstellung eines optimalen Portefeuilles):
a) Positive Aspekte: Die Meriten einer so verstandenen Portfolio Selection werden vor allem unter Einbeziehung einer sog. "risikolosen Anlagemöglichkeit" deutlich: Dadurch gelang zum einen die Ableitung des Tobinschen Separationstheorems im Sinne des Two-Fund-Theorems (im traditionellen Verständnis). Zum anderen und in Zusammenhang damit sind aus der Annahme, dass sich die rationalen, risikoscheuen Anleger genauso verhalten wie es ihnen die Portfolio-Theorie empfiehlt, die zentralen Teile der modernen Kapitalmarkttheorie mit ihrem Kern, dem Capital Asset Pricing Model (CAPM), entstanden. Der Kreis schließt sich, nachdem das CAPM wiederum die Grundlage für die theoretische Fundierung der Risikozuschläge in der modernen Kapitalkostentheorie geliefert und damit letztendlich diejenige Methode im nachhinein legitimiert hat, deren Überlebtheit gerade durch die Portfolio-Theorie bereits erwiesen zu sein schien.

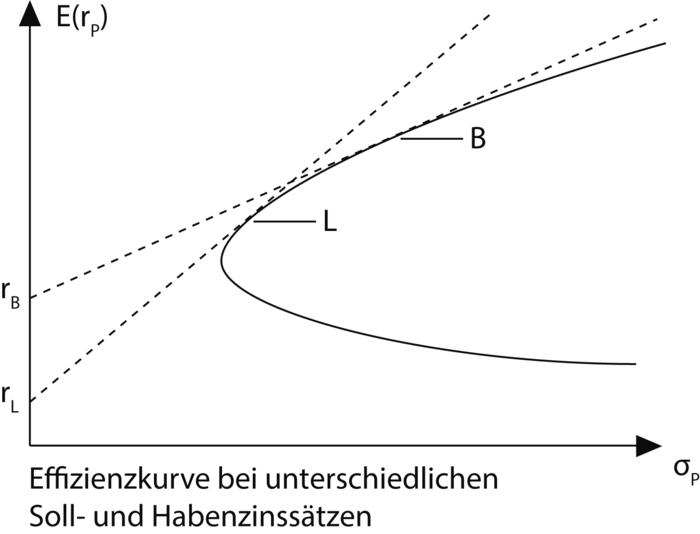
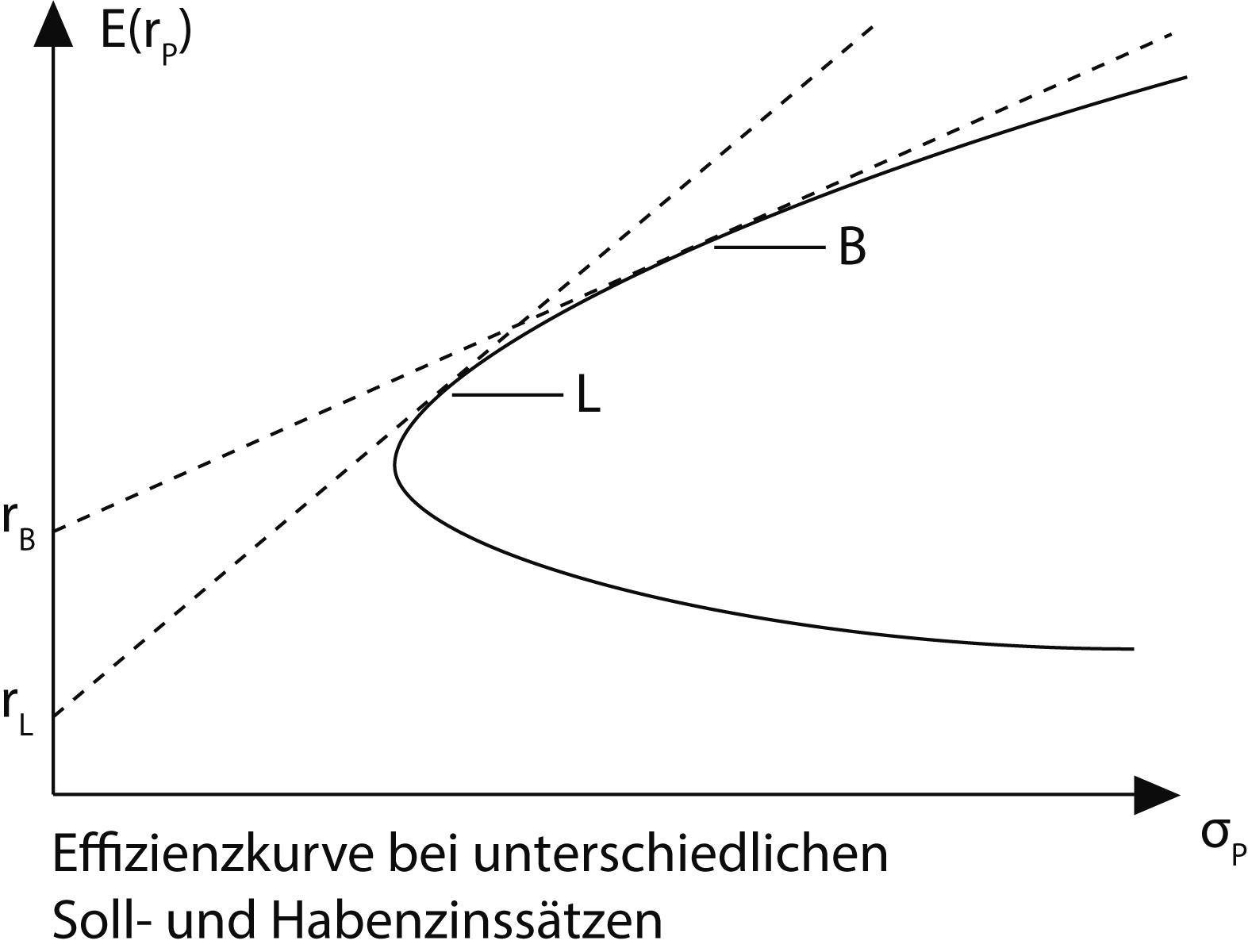
b) Kritische Aspekte: Die ursprüngliche Idee der Portfoliooptimierung durch Gegenüberstellung der Effizienzkurve mit dem System von Rendite-Risiko-Indifferenzkurven des Anlegers unterliegt erheblichen praktischen Anwendungsproblemen (vgl. Portfolio Selection). Diese konnten zwar durch die Annahme einer "risikolosen Anlage" zum Teil überwunden werden, allerdings steht deren Existenz mehr denn je in Frage; vgl. Minimumvarianzportefeuille. Unmittelbar unrealistisch erscheint vor allem aber die weitergehende Annahme der Möglichkeit einer unbeschränkten Kreditaufnahme zu einem gleichen Zins wie dem der risikolosen Anlage. Ohne diese Annahme bricht zwar die Basis für die Ableitung des CAPM (in seiner traditionellen Form) zusammen, aber für die Zwecke der Portfolio-Theorie kann die Portfoliooptimierung durchaus entlang einer neuen, zusammengesetzten Effizienzkurve erfolgen: Die Abbildung zeigt, dass ein stärker risikoscheuer Anleger im Tangentialportfolio L und einer risikolosen Anlage zum Zinssatz r_L investiert sein wird, während ein weniger risikoscheuer Anleger das Tangentialportfolio B hält und dies zum Teil durch Kreditaufnahme zum annahmegemäß höheren Zinssatz r_B finanziert (bevor eine exogene Verschuldungsobergrenze greifen mag). Nur Anleger mit mittlerer Risikoscheu investieren entlang der ursprünglichen Effizienzkurve. Somit bleibt die Portfolio-Theorie auch für diese realistischere Konstellation anwendbar.

Vgl. auch Portfolio-Theorie, Weiterentwicklungen.