Portfolio-Theorie, statistische Methoden
Übersicht
zuletzt besuchte Definitionen...
Im Grundmodell der Portfolio-Theorie von Markowitz wird versucht, einzelne Wertpapieranlagen zu einem effizienten Portefeuille zusammenzustellen und dabei eine eindeutige Beziehung zwischen dem Risiko und der Rendite effizienter Portefeuilles herzuleiten. Die Zusammenstellung effizienter Portefeuilles erfolgt unter der Annahme, dass Anleger bei gleichem erwarteten Ertrag die Anlage mit dem geringeren Risiko bzw. bei gleichem Risiko jene Anlage mit dem höheren erwarteten Ertrag bevorzugen (Effizienzkriterien). Der Ertrag wird als Periodenrendite definiert und das Risiko als Varianz bzw. Standardabweichung der Periodenrendite. Hierbei konzentriert sich Markowitz auf Aktienportefeuilles und unterstellt, dass die zukünftigen Erträge einer Aktienanlage statistisch als Zufallsgröße zu interpretieren sind, die innerhalb bestimmter Grenzen zufällig schwanken. Je größer die Ertragsschwankungen sind, desto größer werden die statistischen Größen Varianz und Standardabweichung, mit denen das Risiko in der Portfolio-Theorie gemessen wird. Ohne weitere Annahmen (Mean-Variance-Approach) muss im Grundmodell unterstellt werden, dass die erwarteten Renditen einer Normalverteilung folgen.
Markowitz konnte erstmals anhand eines einfachen parametrischen Modells den bereits früher bekannten Diversifikationseffekt quantifizieren, dass durch Erhöhung der Anzahl der im Portefeuille befindlichen Aktien das Gesamtrisiko im Vergleich zur Summe der Einzelrisiken reduziert werden kann, sofern die Erträge nicht vollständig positiv miteinander korreliert sind, also kein Korrelationskoeffizient von eins vorliegt. Diversifikation setzt also einen Korrelationskoeffizienten kleiner als eins voraus. Bei perfekt negativer Korrelation wäre bei einer bestimmten Wertpapiermischung sogar eine Verminderung des Portefeuille-Risikos auf null möglich; ein solches Portefeuille wird als Nullvarianzportefeuille bezeichnet. I.d.R. treten positive Korrelationen auf, die dennoch eine Reduzierung des Gesamtrisikos gegenüber der Summe der Einzelrisiken ermöglichen.
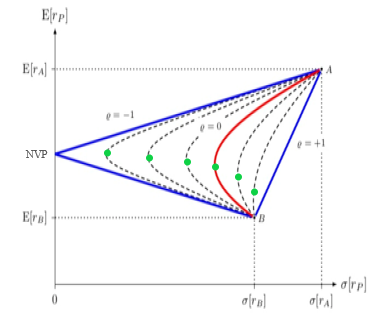
Die Abbildung „Effizienzkurven bei alternativen Korrelationskoeffizienten im 2-Wertpapier-Fall” (modifiziert entnommen aus: Kruschwitz, Lutz: Investitionsrechnung, München 2014, S. 352) zeigt Rendite und Risiko effizienter Portefeuilles bei Korrelationskoeffizienten zweier Wertpapiere A und B in unterschiedlicher Höhe an. Der Zwei-Anlagen-Fall erweist sich zur Verdeutlichung des Diversifikationseffektes als besonders geeignet, weil die Extremfälle vollständig positiver oder negativer Korrelation in ihren Auswirkungen auf die Eigenschaften effizienter Portefeuilles graphisch einfach veranschaulicht werden können: Bei einem Korrelationskoeffizienten von -1 sind die Renditen perfekt negativ korreliert, d.h. die Renditen entwickeln sich vollständig gegenläufig; hierbei hat Wertpapier A ein höheres Risiko als Wertpapier B. In diesem Fall kann das Portefeuille-Risiko bei einer bestimmten Mischung (Nullvarianzportefeuille NVP) gänzlich zum Verschwinden gebracht werden und das Portefeuille einen sicheren Ertrag liefern. Die Gerade zwischen NVP und B stellt die möglichen effizienten Portefeuilles dar, die durch unterschiedlich hohe Anteile der beiden Wertpapiere bestimmt sind. Welches dieser effizienten Portefeuilles ein einzelner Anleger auswählt, hängt von seiner persönlichen Risikoneigung ab (Portfolio Selection). Bei einem Korrelationskoeffizienten von +1 sind die Renditen perfekt positiv korreliert, d.h. entwickeln sich vollständig gleichläufig. Die Gerade zwischen A und B stellt alle effizienten Portefeuilles dar, die ohne die Möglichkeit von Leerverkäufen (Short Sales) realisiert werden können; eine Risikoverminderung durch Diversifikation ist in diesem Fall offenbar nicht möglich, weil sich das Portefeuille-Risiko (gemessen an der additiven Varianz) dann aus der Summe der mit ihren Anteilen gewichteten Einzelrisiken ergibt. Nur bei einem Korrelationskoeffizienten von -1 oder +1 verläuft die Effizienzkurve als Gerade, ansonsten als Kurve i.e.S. Sie verläuft um so weiter links, je kleiner der Korrelationskoeffizient ist und je mehr sich damit das Portefeuille-Risiko unter den gewogenen Durchschnitt der Risiken der Einzelanlagen drücken lässt. Das dabei für eine gegebene Korrelation durch geeignete Mischung überhaupt erreichbare effiziente Portefeuille mit dem geringstmöglichen Portefeuille-Risiko wird gemeinhin (auf die Risikokennzahl Varianz bezogen und) als Minimumvarianzportefeuille (MVP) bezeichnet; dieses ist in der Abbildung jeweils durch einen Punkt markiert. Es lässt sich erkennen, dass mit abnehmender Korrelation durch Auswahl des MVP eine immer höhere Rendite bei gleichzeitig niedrigerem Risiko erwartet werden kann.
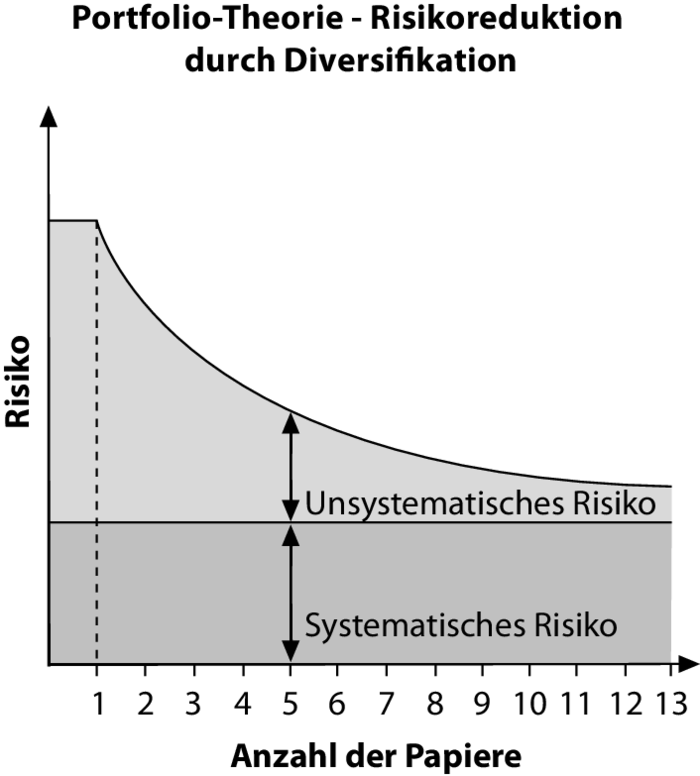
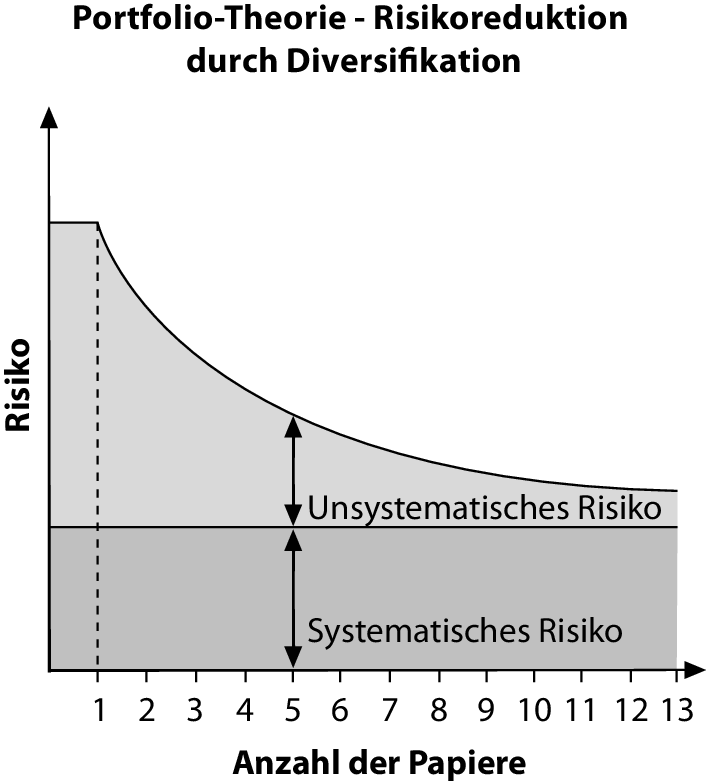
Mit der ersten Abbildung sollte vor allem die große Bedeutung der Korrelation der Renditen einzelner Anlagen für den Diversifikationseffekt in der Portfolio-Theorie nach Markowitz verdeutlicht werden. Die Abbildung „Risikoreduktion durch Diversifikation” basiert demgegenüber auf dem Markt-Modell und zeigt, dass auch jenseits der genauen Betrachtung der Korrelationen das Gesamtrisiko eines Portefeuilles allein durch eine Erhöhung der Anzahl in ihrer Renditeentwicklung nicht vollständig positiv miteinander korrelierter Wertpapiere im Portefeuille verringert werden kann. Je mehr unterschiedliche Wertpapiere (in der idealtypischen Abbildung mit jeweils gleichem Anteil) im Portefeuille gehalten werden, desto geringer wird das Gesamtrisiko. Man spricht hier von naiver Diversifikation im Unterschied zur zuvor behandelten Markowitz-Diversifikation. Bei einer Erweiterung des Portefeuilles nimmt das Risiko zunächst rasch ab, aber bereits ab einer Wertpapieranzahl von ungefähr zehn Werten fällt die zusätzliche Risikoreduzierung zunehmend geringer aus. Die Abbildung zeigt weiter, dass das Gesamtrisiko eines Portefeuilles in zwei Komponenten zerlegt werden kann: das systematische Risiko und das unsystematische Risiko. Nur das unsystematische, also einzeltitelspezifische Risiko kann durch Diversifikation verringert werden. Zurück bleibt das systematische Risiko, das alle Wertpapiere der betrachteten Assetklasse trifft, nur ggf. unterschiedlich stark (und z.B. auf Leitzinsänderungen, Rohstoffpreisentwicklungen wie Ölpreisschocks oder Wahlausgänge zurückgeht). Das systematische Risiko kann nur durch Diversifikation des Portefeuilles über das bisher betrachtete Anlagespektrum, z.B. "deutsche Aktien", hinaus verringert werden, z.B. durch internationale Diversifikation (Asset Allocation, internationale Diversifikation) im Wege der Beimischung ausländischer Aktien oder durch Integration weiterer Assetklassen wie z.B. Zinsinstrumenten oder Rohstoffen.
Literaturhinweise SpringerProfessional.de
Bücher auf springer.com
Interne Verweise
Portfolio-Theorie, statistische Methoden
Portfolio-Theorie, statistische Methoden
- Asset Allocation, Internationale Diversifikation
- Diversifikation
- Diversifikation
- effizientes Portefeuille
- Effizienzkriterien
- Gesamtrisiko
- Korrelationskoeffizient
- Markt-Modell
- Mean-Variance-Approach
- Minimumvarianzportefeuille
- Normalverteilung
- Periodenrendite
- Portfolio Selection
- Portfolio-Theorie
- Short Sales
- Standardabweichung
- systematisches Risiko
- unsystematisches Risiko
- Varianz
- Volatilität
- Zufallsgröße