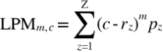Lower Partial Moments (LPM)
Übersicht
zuletzt besuchte Definitionen...
1. Begriff und Einordnung: statistisches Messkonzept, das die wichtigsten downside orientierten Risikomaße (Downside Risk) in einem einheitlichen Analyserahmen integriert, in dem nur negative Abweichungen einer Zufallsvariablen von einer bestimmten Schranke (Schwellenwert, threshhold level) erfasst und als "Risiko" aufgefasst werden. Speziell auf dem Gebiet der Kapitalanlage und dahingehender Renditebetrachtungen wird diese Schranke in einer (geforderten) Mindestrendite gesehen, deren Unterschreitung einen Shortfall darstellt (Shortfall-Risiko). Sie wird entweder je nach Anwendungszusammenhang als plausible ökonomische Größe exogen vorgegeben oder gemeinsam mit der Shortfall-Risikokennzahl, dann typischerweise als Renditeerwartungswert, ermittelt; vgl. Shortfall Threshhold Level zu den gängigsten Mindestrenditegrößen.
2. Terminologie: Dem Anglizismus "Shortfall(-Risiko)" im Sinne eines Versagens, Scheiterns oder Mangels wird mit Absicht der Vorzug gegenüber der üblichen deutschen Übersetzung mit "Ausfall(-Risiko)" gegeben, da diese eine unangemessen enge Assoziation zum Begriff des Adressenausfallrisikos und ggf. auch zum Begriff des Eigenkapitalbedarfs (zur Verhinderung des Ausfalls einer Institution oder zur Einhaltung dahingehender regulatorischer Vorgaben) wecken kann. Ein unerwünschter Shortfall kann statt dessen z.B. auch in einem nominalen oder realen Kapitalverzehr oder einer Unterrendite gegenüber einer Benchmark gesehen werden.
3. Grundidee und Berechnung: Allen Shortfall-Risikomaßen ist die Grundidee gemein, dass vom Risikoempfinden der meisten Kapitalanleger her nur Unterschreitungen einer bestimmten Rendite als "Risiko" angesehen, höhere Renditen aber eher als Chance begriffen werden; bei den auf das Gesamtrisiko bezogenen Risikomaßen der Varianz, der Standardabweichung und der mittleren absoluten Abweichung werden – entgegen dieser Intuition – Renditeabweichungen (vom Erwartungswert) nach oben wie nach unten gleichbehandelt. Hiervon ausgehend unterscheiden sich die einzelnen Shortfall-Risikomaße darin, wie das Ausmaß dieser Unterschreitungen berücksichtigt wird: allgemein in LPM unterschiedlichen Grades (oder unterschiedlicher Ordnung) m bezüglich der (vereinfachend: zeitinvariablen) Mindestrendite c, konkret am anschaulichen Beispiel einer diskreten Zufallsgröße:
für rz < c, wobei: rz = Rendite beim Eintritt des Zustandes z und pz = Wahrscheinlichkeit für Zustand z mit Σ pz= 1.
In der Praxis werden üblicherweise drei Spezialfälle betrachtet: Das LPM nullten Grades (m = 0) wird als Shortfall-Risiko i.e.S. oder auch Shortfall-Wahrscheinlichkeit bezeichnet (Wahrscheinlichkeit, dass die Mindestrendite unterschritten wird, und zwar unabhängig vom Umfang der zu erwartenden Unterschreitung). Für das LPM ersten Grades (m = 1) ist die Bezeichnung als Shortfall-Erwartungswert gebräuchlich; er beschreibt die mittlere Unterschreitungshöhe, und zwar keineswegs auf die Fälle der Unterschreitung selbst beschränkt. Leider wird ein so verstandener Shortfall-Erwartungswert als unbedingtes Shortfall-Risikomaß schnell rein sprachlich mit dem sog. Expected Shortfall als bedingtem Risikomaß verwechselt, was sich mit dem weitergehenden Anglizismus "Average Shortfall" (oder – korrekt, aber unüblich – mit "mittlerer/durchschnittlicher Shortfall") vermeiden ließe. Zudem entzieht sich ein unbedingtes, also gar nicht auf die Fälle des Shortfall selbst beschränktes Shortfall-Maß rasch eines intuitiven Zugangs (außer für m = 0). Schließlich wird das LPM zweiten Grades (m = 2) als Shortfall-Varianz bezeichnet und beschreibt anstelle der mittleren die mittlere quadratische Unterschreitungshöhe; auf diese Weise werden größere Mindestrendite-Unterschreitungen relativ stärker gewichtet als kleinere Abstände, was der grundsätzlich angenommenen Risikoaversion der Anleger gerecht wird. Hierbei stellt die Semivarianz einen Spezialfall dar, in dem als Mindestrendite der Renditeerwartungswert festgelegt wird. Der leichteren Interpretation halber (vgl. Standardabweichung) wird häufig auch das Risikomaß der Shortfall-Standardabweichung (oder Downside-Standardabweichung) eingesetzt, die sich als Quadratwurzel der Shortfall-Varianz ermitteln lässt; entsprechend bezeichnet die Semistandardabweichung wiederum den Spezialfall mit der Mindestrendite als Renditeerwartungswert.
4. Theorieentwicklung: Seit den 1950er-Jahren ist die Entwicklung shortfall-orientierter Risikomaße im wesentlichen von der Diskussion über die zweckmäßige Behandlung der Risikodimension innerhalb der modernen Portfolio-Theorie vorangetrieben worden. In unterschiedlichen sog. Safety-First-Ansätzen wurden Auswahlregeln vorgestellt, nach denen (in herkömmlichem Sinne: µ-σ-) effiziente Portfolios speziell anhand ihrer Shortfall-Wahrscheinlichkeit beurteilt werden. Auch Markowitz selbst war – in kritischer Reflektion des von ihm selbst maßgeblich populär gemachten Mean-Variance-Approach – sogar mit einer ausschließlich shortfall-orientierten Risikomessung befasst und hat bereits in seinem Basiswerk von 1959 konkret eine semivarianzbasierte Methode zur Portfoliooptmierung vorgelegt. Die Verallgemeinerung zu dem einheitlichen LPM-Analyserahmen und parallel dazu zu einem sog. Mean-LPM-Approach einschließlich dessen nutzentheoretischer Fundierung, letztendlich die Anbindung an die moderne Kapitalmarkttheorie mit ihrem Herzstück, dem Capital Asset Pricing Model, erfolgte dann von den 1970er- bis 1990er-Jahren u.a. durch Autoren wie Bawa(/Lindenberg) und Harlow(/Rao).
5. Nutzentheoretische Hinweise: Essentiell für die sinnvolle Anwendbarkeit eines Mean-LPM-Approach ist die Vereinbarkeit des gewählten LPM-Maßes mit einem für rational gehaltenen Entscheidungsverhalten unter Unsicherheit; vgl. Mean-LPM-Approach. Der Grad/die Ordnung eines LPM muss keineswegs ganzzahlig sein, wie Fishburn (1977) in seinem sog. α-t-Modell dargelegt hat. So kann innerhalb des LPM-Rahmenkonzepts je nach Wahl des Grades m ganz unterschiedlichen angenommenen Risikoeinstellungen von (repräsentativen) Anlegern Rechnung getragen werden: Mit "0 < m < 1" wird Risikofreude, mit "m = 1 (oder 0)" Risikoneutralität und mit "m > 1" Risikoaversion/-scheu, jeweils unterhalb der Mindestrendite, zum Ausdruck gebracht, wobei speziell m um so höher angesetzt werden sollte, je größer die Risikoscheu der Anleger eingeschätzt wird. Die weitergehende Diskussion gilt u.a. der Modellierung der Risiko-, besser: Chanceneinstellung oberhalb der Mindestrendite.
Vgl. für den Zusammenhang der Lower Partial Moments zu den Konzepten des Value-at-Risk die Ausführungen zum Shortfall-Risiko und zum Shortfall-Erwartungswert.
Literaturhinweise SpringerProfessional.de
Bücher auf springer.com
Interne Verweise
Lower Partial Moments
Lower Partial Moments
- Adressenausfallrisiko
- Average Shortfall
- Average Shortfall
- Benchmark
- Capital Asset Pricing Model (CAPM)
- diskrete Zufallsgröße
- Downside Risk
- effizientes Portefeuille
- Erwartungswert
- Expected Shortfall
- Gesamtrisiko
- Mean-LPM-Approach
- Mean-LPM-Approach
- Mean-Variance-Approach
- Portfolio-Theorie
- Safety-First-Ansätze der Portfoliooptimierung
- Semistandardabweichung
- Semivarianz
- Shortfall Threshold Level
- Shortfall-Erwartungswert
- Shortfall-Erwartungswert
- Shortfall-Varianz
- Standardabweichung
- Value-at-Risk (VaR)
- Varianz
- Wahrscheinlichkeit P(E)
- Zufallsgröße