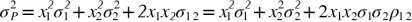Portefeuille-Varianz
Übersicht
zuletzt besuchte Definitionen...
Summe der mit ihrem gemeinsamen Anteil (Produkt) am Portefeuille gewogenen Gleich- oder Gegenläufigkeit der Renditeentwicklung jeweils zweier Anlagen, bei der über alle Anlagepaare eines Portefeuilles aufsummiert wird. Als Gleichlaufmaß wird hierbei die Kovarianz benutzt, die im Unterschied zum Korrelationskoeffizienten die Additivitätseigenschaft aufweist; dabei lässt sich die Varianz (einer Einzelanlage) als spezielle Kovarianz, nämlich als Kovarianz der Rendite einer Einzelanlage mit sich selbst interpretieren:
wobei:
σP2 = Portefeuille-Varianz
xi, xj = Anteile der Anlage i bzw. j am Portefeuille
σij = Kovarianz der Renditen der Anlagen i und j (falls i = j: σii = σi2 = Varianz der Rendite der Anlage i).
Es lässt sich erkennen, dass die Bedeutung speziell der Varianz (bzw. Standardabweichung) der Rendite einer Einzelanlage als traditionelle Risikokennzahl im Portfoliozusammenhang mit einer zunehmenden Anzahl von Anlagen im Portefeuille von der Rolle der Kovarianzen überlagert wird und damit (überproportional) zurückgeht. Im Zwei-Anlagen-Fall lässt sich die Portefeuille-Varianz mit folgender Formel ermitteln:
wobei (zusätzlich zur generellen Formel):
σ1, σ2 = Standardabweichung der Rendite der Anlage 1 bzw. 2
ρ12 = Korrelationskoeffizient der Renditen der Anlagen 1 und 2.
Da im Zwei-Anlagen-Fall x2 = 1–x1 gilt, lässt sich so der Verlauf der Effizienzkurve in Abhängigkeit vom Korrelationskoeffizienten analytisch ableiten; vgl. zu einer entsprechenden Abbildung Portfolio-Theorie, statistische Methoden. Im Mehr-Anlagen-Fall bedarf es zur Ermittlung der Effizienzkurve je nach Nebenbedingungen unterschiedlich komplexer Verfahren der quadratischen Programmierung zur Minimierung der Portefeuille-Varianz bei parametrisch gegebenem Erwartungswert der Portefeuille-Rendite.