Portfolio Selection

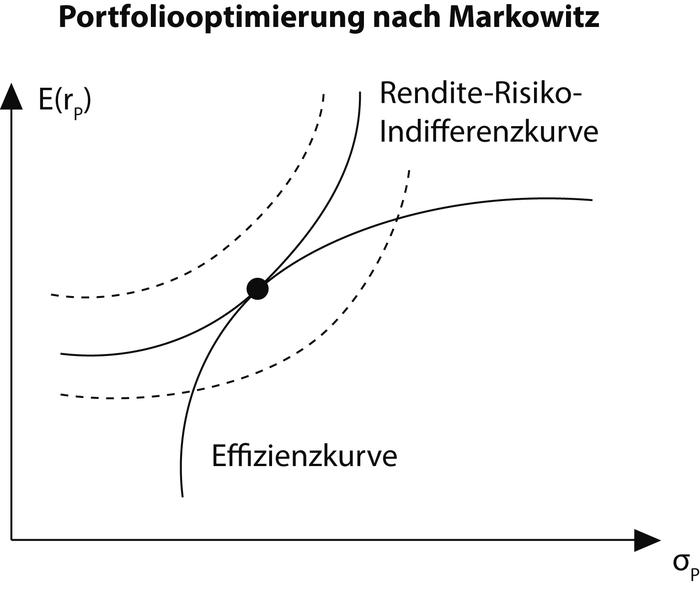
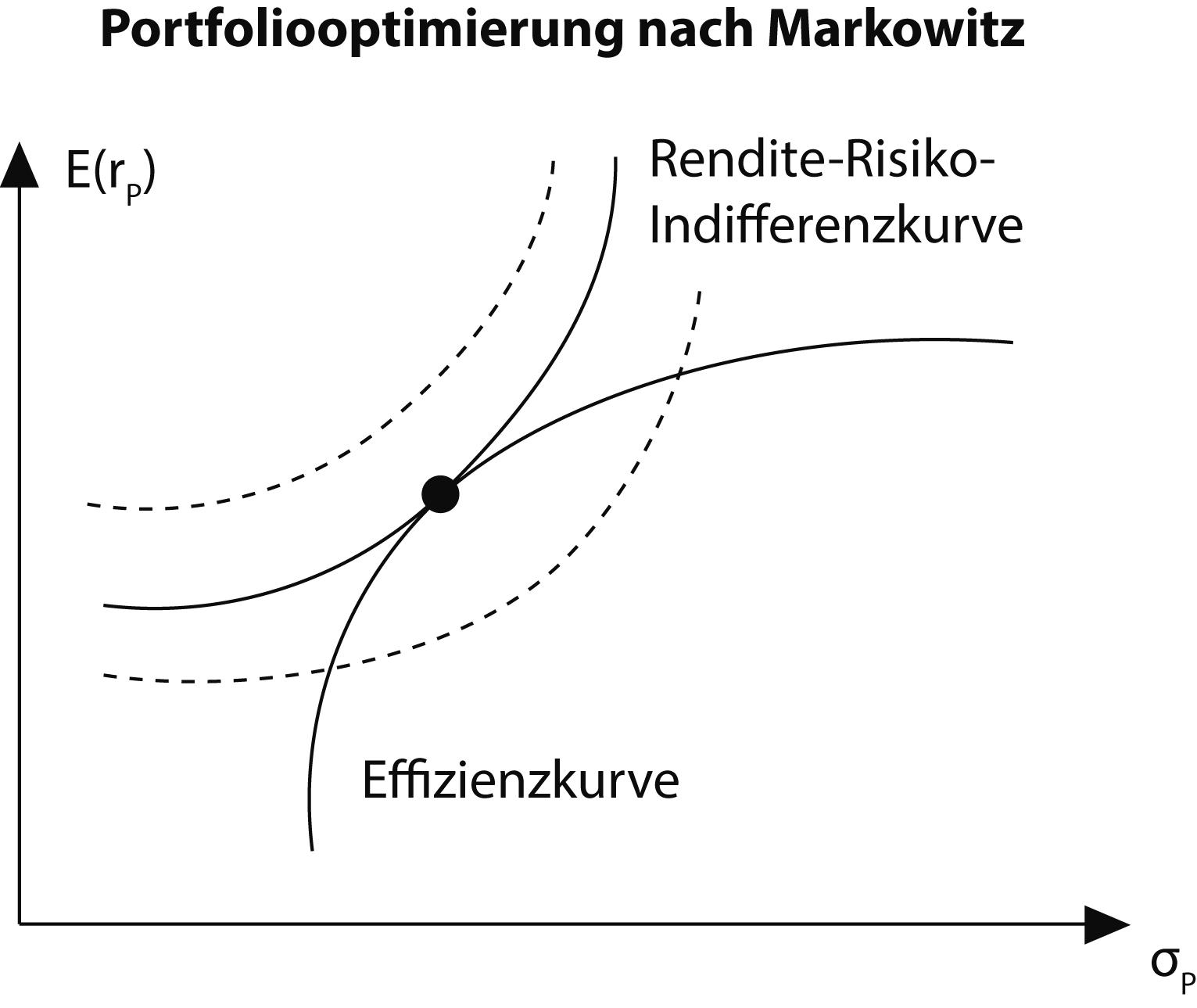
wichtiger Bestandteil der Portfolio-Theorie (i.w.S.), der von Markowitz ausgehenden Theorie der unter Diversifikationsaspekten optimalen Zusammenstellung eines Wertpapier-Portfolios. In der Portfolio-Theorie i.e.S. ergibt sich auf mathematisch-statistischer Basis (Portfolio-Theorie, statistische Methoden) und unter Heranziehung eines Effizienzkriteriums eine Vielzahl sog. effizienter Portefeuilles, deren geometrischer Ort im Rendite-Risiko-Raum (als μ-σ-Raum) durch eine Effizienzkurve abgebildet wird. Markowitz selbst hatte zunächst schlicht dazu aufgerufen, dass der Investor aus diesen effizienten Portefeuilles dasjenige auswählen möge, das seiner Risikopräferenz am ehesten entspricht. Später ist weithin üblich geworden, dieses Entscheidungsproblem unter Rückgriff auf das Instrumentarium der modernen Entscheidungstheorie zu behandeln: durch Gegenüberstellung der Effizienzkurve mit dem System von Rendite-Risiko-Indifferenzkurven als geometrische Orte vom Entscheider gleich wertgeschätzter Rendite-Risiko-Kombinationen. Das optimale Portefeuille ergibt sich dann als Tangentialpunkt der weitestmöglich außen liegenden und damit das höchste erreichbare Nutzenniveau repräsentierenden Indifferenzkurve mit der Effizienzkurve, wie die Abbildung "Portfoliooptimierung nach Markowitz" zeigt.

Bild in Originalgröße zeigen

Über die konzeptionelle Problematik dieses Ansatzes (Mean-Variance-Approach) hinaus stößt allerdings die Handhabung des Instrumentariums auf vielfältige praktische Probleme u.a. bei der Erhältlichkeit des Indifferenzkurvensystems (bes. bei Gruppenentscheidungen) sowie seiner Stabilität im Zeitablauf. Vor diesem Hintergrund kommt der Erweiterung des Modells von Markowitz durch Tobin im Jahre 1958 richtungsweisende Bedeutung zu: Dann, wenn eine sog. "risikolose Anlagemöglichkeit" existiert, ergibt sich eine völlig neue, und zwar linear verlaufende Effizienzkurve, deren Portefeuilles nur noch aus Mischungen dieser risikolosen Anlage mit einer einzigen optimalen Kombination risikobehafteter Wertpapiere, dem sog. Tangentialportefeuille, bestehen. Existiert weiterhin die Möglichkeit zu einer unbeschränkten Kreditaufnahme zu gleichen Konditionen, umfasst die Effizienzkurve auch kreditfinanzierte Investitionen in dieses Portefeuille; dieser Zusammenhang wird als Two-Fund-Theorem bezeichnet. Demnach lässt sich der risikobehaftete Teil des Portefeuilles unabhängig von der Risikoeinstellung des Investors – und damit ohne deren Kenntnis, bspw. im Investmentgeschäft – optimieren; seiner individuellen Risikopräferenz kann der Investor dann durch Beimischung einer risikolosen Anlage (für den Fall stärkerer Risikoscheu) bzw. durch Kreditfinanzierung seiner Investition (für den Fall geringer ausgeprägter Risikoscheu) Rechnung tragen. Dass die Voraussetzungen hierfür in der Praxis offenbar nicht gegeben sind, lässt sich u.a. am Angebot nach Risikoklassen gestaffelter Anlageprodukte ("chancenorientiert", "sicherheitsorientiert" etc.) in der standardisierten Vermögensverwaltung erkennen. Unabhängig davon kann auch der Fall eines höheren Kredit- als Anlagezinssatzes in dem Modellrahmen implementiert werden; vgl. Portfolio-Theorie, Modellbeurteilung, Ziff. 2.b)).

Aus pragmatischer Sicht kann zudem die Einbeziehung von Optionen Abhilfe schaffen: Auch ohne eine risikolose Anlage- und (vor allem) Verschuldungsmöglichkeit zu gleichen Konditionen ergibt sich eine neue, oberhalb der ursprünglichen verlaufende Effizienzkurve: mit tief im Geld (vgl. Moneyness) geschriebenen (und fast sicher ausgeübten) Covered Calls über aus dem Geld geschriebenen Covered Calls, dem Underlying stand alone, In-the-Money-Calls bis hin zu Deep-out-of-the-Money-Calls (Puts jeweils umgekehrt analog) mit einem "Quasi-Marktportefeuille" als Basiswert  – "quasi", weil das Grundmodell der Portfolio-Theorie und damit auch das Capital Asset Pricing Model (CAPM) in seiner Grundversion bei Einbeziehung von Optionen nicht mehr sinnvoll angewandt werden kann (vgl. Portfolio-Theorie, Modellbeurteiliung, Ziff. 1.b)). Derartige Betrachtungen werden bereits seit den 1970er-Jahren (Ross, Hakansson) – in der normativen Optionspreistheorie – vielmehr auf wohlfahrtstheoretischer Basis (mit dem Time-state-preference-Ansatz) durchgeführt. An das CAPM herangerückt werden sie allerdings durch die Vorstellung, dass die Marktteilnehmer homogene Erwartungen über die Entwicklung der Wertpapierrenditen unter der Bedingung hegen, dass eine bestimmte Entwicklung des Marktportefeuilles eintritt: Die Homogenität dieser bedingten Erwartungen sorgt hier dafür, dass alle Anleger sich nur im Quasi-Marktportefeuille engagieren und allein in (heterogener) Erwartung über dessen Entwicklung die beschriebenen Optionspositionen einnehmen. U.a. die Frage, ob sich hieraus eine marktweite Gesamtposition in allen Optionsserien von Null ergibt und was dies andernfalls bedeutet, führt in tiefe Verästelungen, sogar in kapitalmarktpolitische Handlungsempfehlungen.

Auf alle Fälle sind die Vervollständigung des Kapitalmarktes durch Einbeziehung einer risikolosen Anlage oder – wie auch immer ausgestaltete – Optionen und das Two-Fund-Theorem ganz unabhängig von kapitalmarktgleichgewichtstheoretischen Überlegungen (CAPM) von großer Bedeutung für die praktische Anwendbarkeit der Portfolio-Theorie. Der Begriff des auf seinen Begründer zurückgehenden Tobinschen Separationstheorems wird allerdings heute ganz überwiegend im Rahmen weiterführender gleichgewichtstheoretischer Konzepte, die insbesondere auf der Annahme vollständig homogener Erwartungen der Marktteilnehmer basieren, verwandt. Das oben genannte Tangentialportefeuille lässt sich dann als das sog. Marktportefeuille (im eigentlichen Sinne) identifizieren, die oben genannte lineare Effizienzkurve als sog. Kapitalmarktlinie; vgl. Tobinsches Separationstheorem, portfolioorientierte Aktienanalyse, Asset Allocation, Minimumvarianzportefeuille, Mean-LPM-Approach.