Put-Call-Parität
GEPRÜFTES WISSEN
Über 100 Experten aus Wissenschaft und Praxis.
Mehr als 8.000 Stichwörter kostenlos Online.
Das Original: Gabler Banklexikon
Übersicht
zuletzt besuchte Definitionen...
Put-Call-Parity; 1. Begriff: Die Put-Call-Parität ist eine feste Preisrelation zwischen Puts und Calls gleichartiger Optionen, d.h. von Optionen mit gleichem Basiswert, gleichem Basispreis und gleicher Fälligkeit.
2. Formel: Je nach Typ der Optionen gibt es verschiedene Formen der Put-Call-Parität. Die einfachste Grundform gilt für europäische Optionen auf Aktien, auf die während der Restlaufzeit keine Dividendenausschüttungen entfallen. Die Parität lautet dann:
wobei:
C = Kurs der Call Option (Optionsprämie)
S = Kurs des Basiswertes
X = Basispreis
exp = Exponentialfunktion
r = auf der Basis stetiger Verzinsung berechneter annualisierter Zins
t = Restlaufzeit der Option.
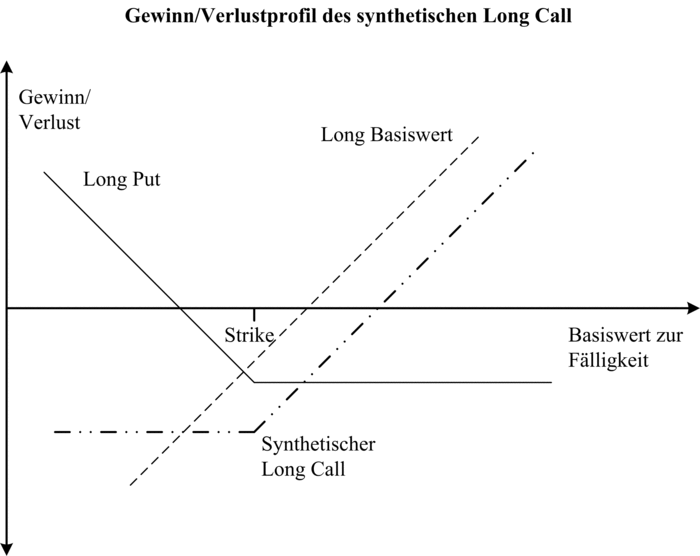
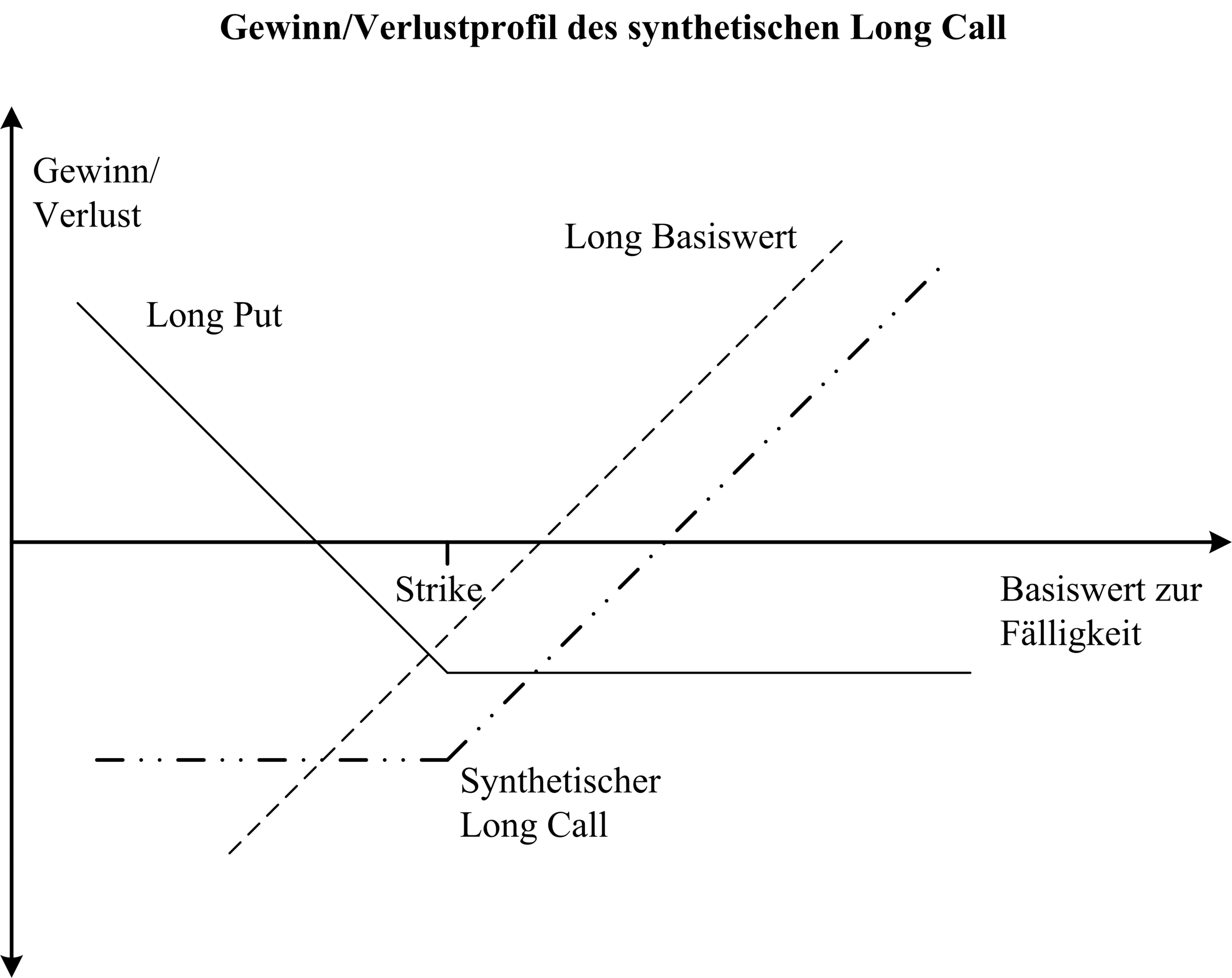
3. Synthetische Positionen: Mithilfe der Relation der Put-Call-Parität lassen sich synthetische Positionen nachstellen. So kann beispielsweise eine synthetische Long-Position im Basiswert (synthetisches Papier) gebildet werden, indem eine Long Call-Position und eine Short Put-Position eingegangen werden. Ausgehend von dieser Grundgleichung kann dann eine Long Call-Position synthetisch gebildet werden, indem eine Long Put-Position und eine Long-Position im Basiswert kombiniert werden. Siehe dazu die Abbildung Gewinn/Verlustprofil des synthetischen Long Call.
Vgl. auch Black-Scholes-Modell.
