Zitierfähige Version
- Revision von Black-Scholes-Modell vom 30.07.2012 - 18:13
- Revision von Black-Scholes-Modell vom 30.10.2018 - 13:14
- Revision von Black-Scholes-Modell vom 24.02.2020 - 10:17
- Revision von Black-Scholes-Modell vom 09.04.2020 - 11:12
- Revision von Black-Scholes-Modell vom 09.04.2020 - 17:45
- Revision von Black-Scholes-Modell vom 14.04.2020 - 15:54
Black-Scholes-Modell
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 100 Experten aus Wissenschaft und Praxis.
Mehr als 8.000 Stichwörter kostenlos Online.
Das Original: Gabler Banklexikon
zuletzt besuchte Definitionen...
Black-Scholes-Merton-Modell; 1. Begriff: Optionspreisbewertungsmodell zur Ermittlung des Fair Value von europäischen Optionen auf Aktien oder Aktienindizes (z.B. Optionen auf den DAX), das 1973 von Fischer Black, Myron Scholes und Robert C. Merton konzipiert wurde.
2. Berechnung: Die folgenden Formeln sind jeweils für den Fall stetiger Verzinsung notiert. Betrachtet man dagegen Zinsfaktoren für den Fall diskreter Verzinsung, so sind die Formeln geeignet anzupassen.
a) Fair Value eines europäischen Calls:
wobei:
C = Kurs der Call Option (Optionsprämie)
S = Kurs des Basiswertes
X = Basispreis
exp = Exponentialfunktion
r = auf der Basis stetiger Verzinsung berechneter annualisierter Zins
σ = Volatilität
t = Restlaufzeit der Option
ln = Logarithmus naturalis
N (d) = Funktionswert der kumulativen Normalverteilung an der Stelle d,wobei gilt
Im Gegensatz zur obigen Formel wird bei dieser Darstellung der Basispreis der Option abgezinst. N(d1) entspricht dem Delta (Delta-Faktor) einer Option. Mit dieser Formel können nicht nur europäische Call-Optionen bewertet werden, sondern auch amerikanische Call-Optionen, die keine Dividendenzahlungen haben. Da amerikanische Kaufoptionen während der Laufzeit immer eine Zeitprämie haben, würde man sich bei vorzeitiger Ausübung immer schlechter stellen. Das zusätzliche Recht der vorzeitigen Ausübung ist damit wertlos.
b) Fair Value einer europäischen Put-Option:
wobei P = Kurs der Put-Option (Optionsprämie) und alle weiteren Symbole wie oben. Die Bewertung einer Put-Option kann auch durch Verwendung der Put-Call-Parität erfolgen. Für den Preis europäischer Optionen gleichen Typs gilt die folgende Parität:
3. Folgende Prämissen liegen dem Black-Scholes-Modell zugrunde:
Es handelt sich um eine europäische Option.
Während der Laufzeit der Option dürfen keine Ausschüttungen erfolgen.
Es existieren keine Transaktionskosten und Steuern und keine Marktzutrittsbeschränkungen, d.h. der Kapitalmarkt ist vollkommen und vollständig. Damit kann das Hedgeportefeuille kontinuierlich gebildet werden und es existiert ein konstanter Kalkulationsszinssatz.
Die logarithmierten Aktienrenditen unterliegen einer Normalverteilung.
Die Momentanvarianz der Kursrenditen ist konstant.
4. Sonderfälle:
a) Bei einer Volatilität von null vereinfacht sich die Call-Gleichung wie folgt, da sowohl N(d1) als auch N(d2) den Wert 1 haben:
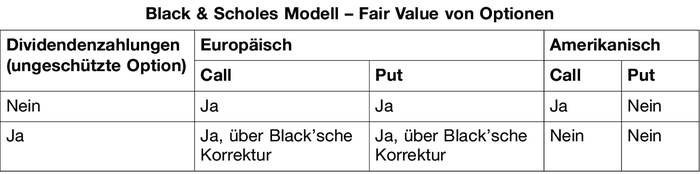
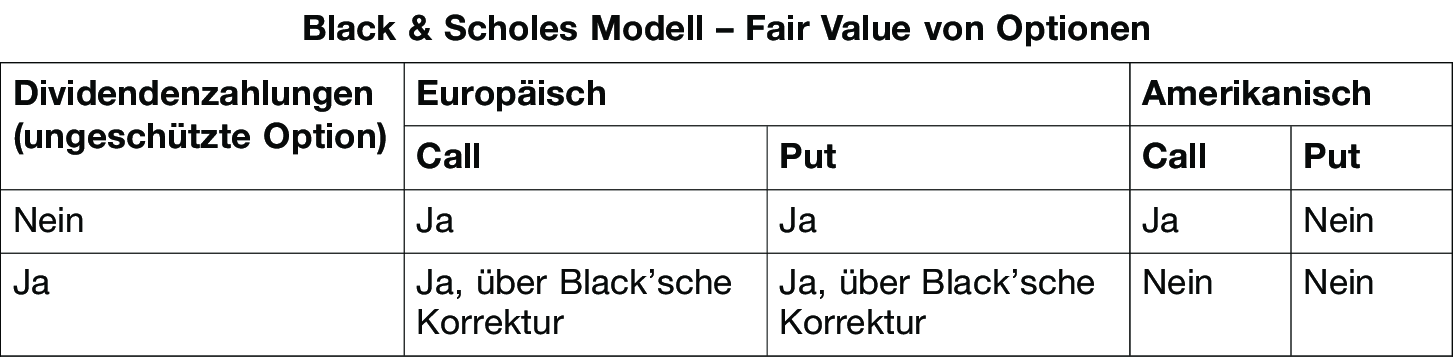
b) Werden entgegen der Prämisse Dividenden ausgeschüttet (Black'sche Korrektur), verringert sich der Fair Value der Call-Option, da der Optionshalter im Gegensatz zum Aktionär keine Dividende erhält. Erfolgen während der Laufzeit einer Option Dividendenzahlungen, führt dies zu Kursabschlägen beim Aktienkurs. Dies bedeutet einen Nachteil für die Long-Position eines Call. Andererseits profitiert eine Put-Option von niedrigeren Aktienkursen, sodass der Fair Value einer Put-Option steigt. Im Fall einer ungeschützten Option, d.h. der Optionsinhaber erhält keine Kompensation, muss die Black-Scholes-Formel deshalb modifiziert werden (Black'sche Korrektur). Bei einer geschützten Option erhält der Optionshaber eine Kompensation. Der Basispreis kann hierbei beispielsweise um die Dividendenhöhe verringert werden. Deshalb brauchen Dividendenzahlungen beim Black-Scholes-Modell nicht berücksichtigt zu werden. Die Tabelle Black-Scholes-Modell - Fair Value von Optionen zeigt, für welche Fälle mit dem Black-Scholes-Modell der Fair Value von Optionen ermittelt werden kann. Das Black-Scholes-Modell ist die Basis für das Black-Modell, das zur Bewertung von Optionen auf Futures konzipiert wurde, und wird nicht nur zur Bewertung von europäischen Aktienoptionen, sondern auch zur Ermittlung des Fair Value von Optionsscheinen auf Aktien verwendet. Modifikationen des Black-Scholes-Modells werden u.a. auch zur Bewertung von Devisenoptionen (Garman-Kohlhagen-Modell) verwendet.
Vgl. auch Cox-Ross-Rubinstein-Modell.

GEPRÜFTES WISSEN
Über 100 Experten aus Wissenschaft und Praxis.
Mehr als 8.000 Stichwörter kostenlos Online.
Das Original: Gabler Banklexikon