Volatility Smile

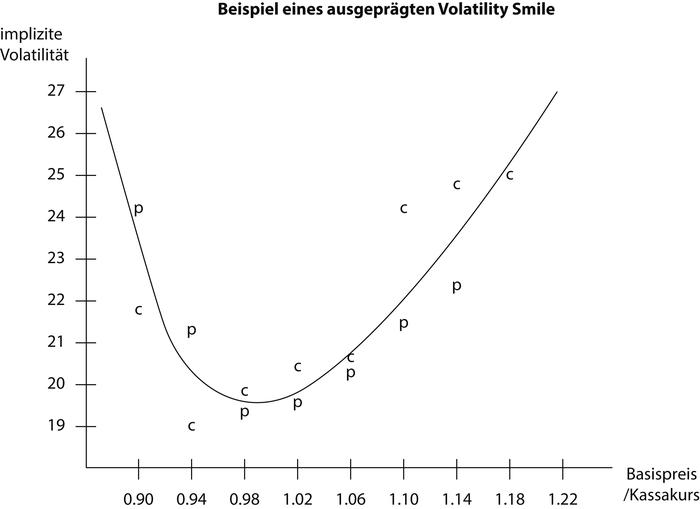
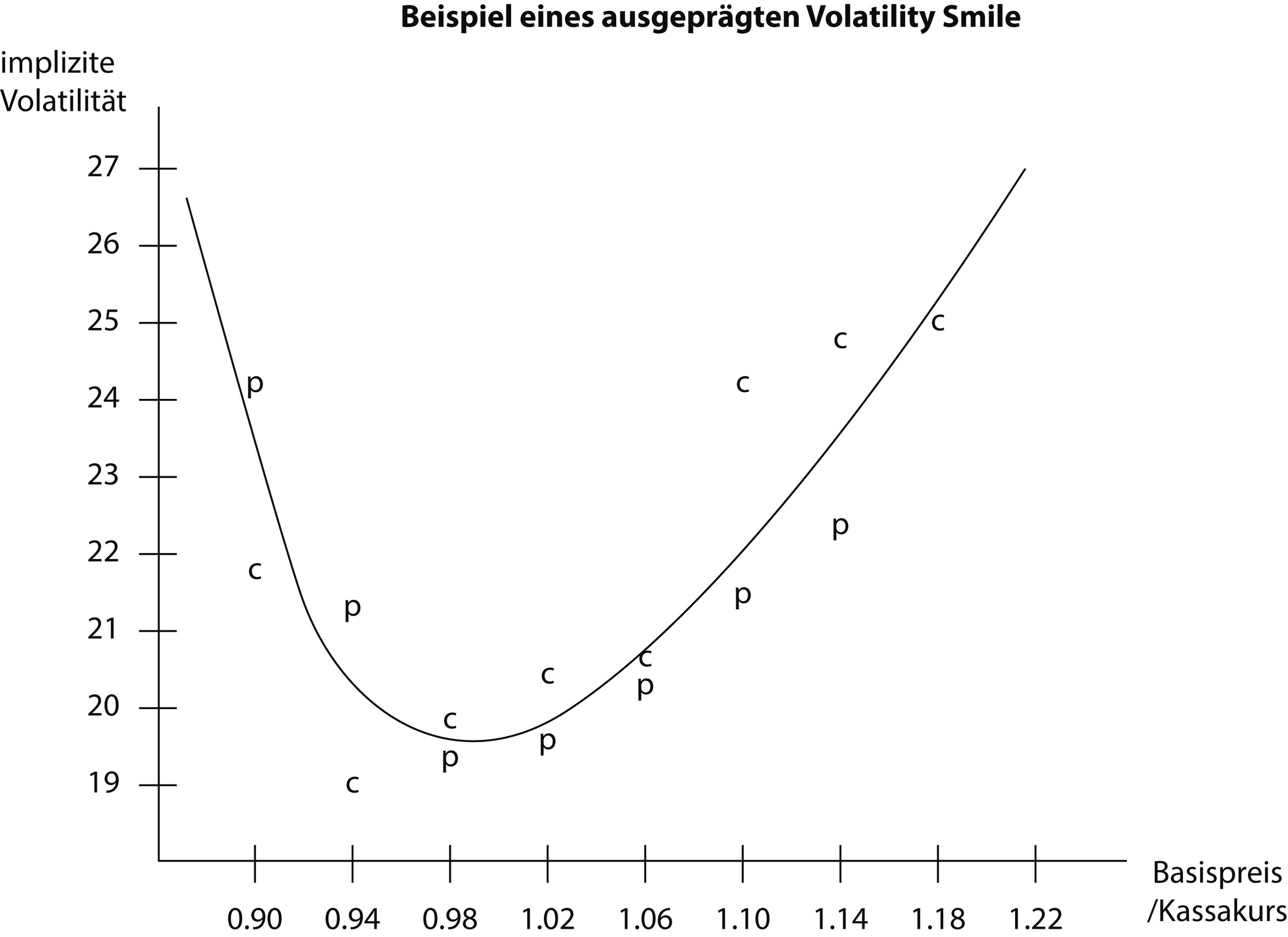
1. Begriff: systematisch zu beobachtendes Verlaufsbild der impliziten Volatilität von Optionsserien gleicher Restlaufzeit in Abhängigkeit vom Basispreisbereich, wonach die implizite Volatilität von At-the-Money-Optionen niedriger ist als die von In-the-Money-Optionen und Out-of-the-Money- Optionen. Die Abbildung auf der nächsten Seite zeigt einen besonders ausgeprägten Smile, der sich aus den einzelnen impliziten Volatilitäten der Puts (p) und Calls (c) in Abhängigkeit von ihrem normierten Basispreis (vgl. Moneyness, Ziff. 4) ergibt. Zu beobachten ist ein derart "klassischer" Volatility Smile am ehesten bei Währungsoptionen und bei Optionen auf Einzelaktien mit einer kurzen Restlaufzeit; ansonsten dominieren Volatility Skews.

Bild in Originalgröße zeigen

Im Beispiel herrscht "Nervosität" im Markt, was instruktiv am Abreißen der Konversionsarbitrage farer out of und in the Money abgelesen werden kann; man erkennt, wie die "Outs" (Out-of-the-Money-Optionen), links die Puts und rechts die Calls, die Flügel ("Wings") des Smile ausprägen.

2. Erklärungsansätze (jenseits "technischer" Faktoren wie Transaktionskosten, Synchronisationsrisiken etc.): Eine wichtige Rolle beim Zustandekommen von Smile-Strukturen wird der Leptokurtosis der Wahrscheinlichkeitsverteilung vieler (Underlying-)Renditen mit ihren sog. "fat tails", relativ (zur Normalverteilung) überdurchschnittlich vielen "Renditeausreißern" nach oben und unten (Portfolio-Theorie, Modellbeurteilung) zugeschrieben, da In- und Out-of-the-Money-Optionen so überproportional an Wert gewinnen (vgl. für eine intuitive Erklärung Skew-Risiko, Ziff. 2). Dies wird in den gängigen Optionsbewertungsmodellen im Geiste von Black/Scholes nicht nachvollzogen, da dort der renditegenerierende (Random-Walk-)Prozess weder kürzerfristige positive Autokorrelationen noch eine stochastische Volatilität vorsieht, so dass diese "Modellfehler" (vgl. implizite Volatilität, Ziff. 3) in einem Volatility Smile auflaufen müssen. Dass es sich hierbei bei Aktienoptionen um ein eher kurzfristiges Phänomen bei erwartbar bevorstehenden starken Kursbewegungen (vgl. Kurtosis-Trading) handelt, unterstreicht dessen Erklärungsbeitrag gerade für die o.g. kurzlaufenden Optionen auf Einzelaktien.

Des weiteren ist eine spezifische Angebotspräferenz zu beobachten: Der hohe Zeitwert von At-the-Money-Optionen (bei Einzelaktien: forward) bzw. Near-the-Money-Optionen (bei Währungen: in Abhängigkeit vom Swapsatz) und dessen Abbau, umgekehrt dessen Vereinnahmung über die Restlaufzeit, gemessen am Theta-Faktor, macht diese für Stillhalter, auch solche mit Volatilitatsprämienstrategien (Volatilitätsstrategien), besonders attraktiv und drückt in diesem Basispreisbereich auf die Preise. Konvexität, gemessen am Gamma-Faktor, ist in diesem Marktsegment also besonders günstig zu erwerben, weil die Stillhalter gleichsam einen "Mengenrabatt" (in Gamma-Einheiten) gewähren. Dies liegt an dem Umstand, dass außerhalb des At-the-Money-Bereichs die Stillhalter eine Prämie für das sog. "dynamische Absicherungsrisiko" verlangen, bei Kursrückgängen im Underlying links und bei Kursanstiegen rechts vom At-the-Money-Bereich immer stärker prozyklisch "nachhedgen" (Delta-Hedging) zu müssen, weil der Gamma-Faktor ansteigt und erst at the Money sein Maximum erreicht. Dort erreicht der sog. Speed, die Veränderung des Gamma in Abhängigkeit vom Kurs des Underlying, sein Minimum (bei Null); diesseits und jenseits davon verzerrt eine Risikoprämie die impliziten Volatilitäten nach oben, die man als "Speed-Prämie" (für das "Speed-Risiko") bezeichnen könnte. Auf der anderen Marktseite scheinen die korrespondierenden Möglichkeiten für das sog. (long) Gamma-Scalping (Volatilitätsstrategien, Ziff. 3.a)), d.h. die antizyklische Glattstellung des durch Kursveränderungen im Underlying "produzierten" Delta, von den Marktteilnehmern noch nicht ausreichend verinnerlicht worden zu sein und/oder von "auskömmlichen" Bid-Ask-Spreads der Market Maker verhindert zu werden.

Mit Blick auf die Hedging-Praxis ist weiterhin von größter Bedeutung, dass parallel zum Gamma-Faktor auch der Vega-Faktor at the Money sein Maximum erreicht: Da der Anpassungsbedarf eines Vega-Hedge in Abhängigkeit vom Kurs des Underlying identisch ist mit dem Anpassungsbedarf eines Delta-Hedge in Abhängigkeit von der impliziten Volatilität, stellt sich das dahingehende Vanna-Hedging (vgl. Skew-Risiko, Ziff. 3) als unproblematisch dar, wenn die implizite Volatilität und die Rendite des Underlying unabhängig voneinander sind. Dies ist allerdings i.d.R. nicht der Fall und trägt ja maßgeblich zur Etablierung einer Skew-Struktur bei (vgl. Volatility Skew, Ziff. 2 a.E.); innerhalb dieser wird sich diesseits und jenseits des At-the-Money-Bereichs damit eine neuerliche Prämie für ein dynamisches Absicherungsrisiko als "Vanna-Prämie" ergeben: Das "Nachhedgen" auf einen Anstieg der impliziten Volatilität hin (wegen des via Vanna gestiegenen Delta) besteht bei Long-Positionen in Calls und Short-Positionen in Puts in einem Verkauf des Underlying, und zwar in einen fallenden Markt hinein, der auf Reverse-Skew-Märkten idealtypisch mit einem Anstieg der impliziten Volatilität einhergeht; gleiches gilt für den umgekehrten Fall (strengenommen ließe sich dies durch gezieltes Unterhedging [bei Calls] vermeiden [vgl. Shadow Delta]; für diesen Fall wäre das sog. Zomma, die Veränderung des Vanna bei Kursveränderungen des Underlying, zu analysieren). Bei Long-Positionen in Puts und Short-Positionen in Calls ergibt sich demgegenüber vielmehr eine "dynamische Absicherungschance", die letztlich einer Smile-Struktur entgegenwirkt; in der Tat ist in der Abbildung im At-the-money-Bereich zu erkennen, wie die dortige Vermeidung des Absicherungsrisikos eher auf die Put-Preise drückt, während bei unvollständiger Konversionsarbitrage (s.o.) die Stillhalter von Calls offenbar einen Ausgleich dafür kalkulieren, dass sie dort um ihre Absicherungschance gebracht sind. Bemerkenswerterweise nimmt – im Gegensatz zu Vega – die Bedeutung des Vanna (parallel zu Gamma) mit abnehmender Restlaufzeit zu; dessen Erklärungsbeitrag wird damit gerade für die eingangs genannten Kurzläufer unterstrichen. Demgegenüber kann analog für Langläufer eine "Volga-Prämie" (vgl. Skew-Risiko, Ziff. 3) veranschlagt werden.

All diese Aspekte sind im übrigen auch auf Märkten mit einer Skew-Struktur wirksam und bleiben zu einem großen Teil bzw. zumeist nur deshalb unsichtbar, weil sie von den vorherrschenden Asymmetrien (Volatility Skew) überdeckt werden. Wenn sie erkennbar sind, wird von einem Volatility Smirk gesprochen.