Volatility Skew
Übersicht
zuletzt besuchte Definitionen...
1. Begriff: Oberbegriff für verschiedene systematisch zu beobachtende Verlaufsbilder der impliziten Volatilität von Optionsserien gleicher Restlaufzeit in Abhängigkeit vom Basispreisbereich (Vertical Skew, Strike Skew) oder von Optionsserien mit gleichem Basispreis in Abhängigkeit von der Restlaufzeit (Horizontal Skew, Time Skew). Nehmen die impliziten Volatilitäten bei gegebener Restlaufzeit mit zunehmendem Basispreis oder bei gegebenem Basispreis mit zunehmender Restlaufzeit kontinuierlich ab, ist von einem Reverse Skew (oder Volatility Sneer) die Rede; eine Situation, in der sie kontinuierlich zunehmen, wird als Forward Skew bezeichnet. Die Märkte, auf denen ein Skew zu beobachten ist, mögen als "Skew-Märkte" bezeichnet werden.
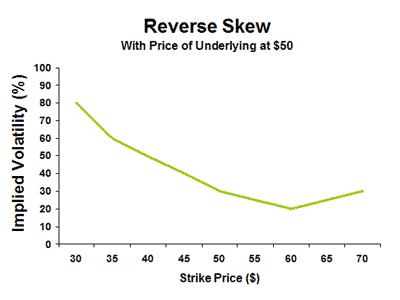
2. Zum Reverse Vertical Skew: Dieses in Theorie und Praxis meistdiskutierte Skew-Phänomen ist regelmäßig bei Optionen auf Einzelaktien mit einer längeren Restlaufzeit sowie generell bei Aktienindex-Optionen und den korrespondierenden Futures-Optionen zu beobachten. Die Abbildung auf der nächsten Seite zeigt einen realtypischen Reverse Skew, hier für eine fortgeschrittene Marktphase in einem Abwärtstrend:
Zweitens entscheidet die Nettoposition des Marktes im Underlying über das Risikoprofil von Stillhalter-Strategien sowie über die dominierende Richtung der Absicherungsbedarfe, die auf Wertpapiermärkten wegen des positiven Nettobestandes im Underlying downside orientiert sind. Konkret wird der Erwerb von Out-of-the-Money-Puts zu Absicherungszwecken favorisiert, demgegenüber das Angebot von "nackten Puts" im allgemeinen und in diesem Marktsegment im besonderen wegen des damit verbundenen hohen Verlustrisikos (gemessen an der Optionselastizität; ansonsten gilt: "Covered Call = Short Put + risikolose Anlage" nach der Put-Call-Parität) zurückbleibt. Um diesen Kauf zu refinanzieren, neigen überdies zahlreiche institutionelle Anleger dazu, möglichst weit, d.h. soweit es der gewünschte Cashflow von null erlaubt, aus dem Geld liegende Calls zu schreiben, woraus sich das vielfach attraktiv erscheinende Erfolgsprofil eines Zero Cost Collar ergibt. Jedenfalls bewirkt das Überangebot in diesem Marktsegment einen dortigen Preisverfall und setzt damit den generellen Käufermarkt (vgl. Volatility Smile), der durch die Generierung von Optionsprämien (im Wege des Covered Writing) geprägt und insgesamt eher im Slightly-out-of-the-Money-Bereich (Moneyness) zu verorten ist, in den "Farer-out-of-the-Money-Bereich" fort.
Drittens stehen sich im gegenüberliegenden Marktsegment eine hohe Nachfrage nach In-the-Money-Calls als attraktive, weil "leveraged" Alternative zur Investition im Basiswert, und ein bescheidenes Angebot gegenüber, weil dort weder Zeitwert vereinnahmt noch Theta generiert werden kann. Die relativ hohe Nachfrage nach In-the-Money-Calls – und in der Folge nach Out-of-the-Money-Puts durch Konversionsarbitrage – gegenüber einer niedrigen Nachfrage nach In-the-Money-Puts ist letztlich durch die quantitative Geldpolitik getrieben, die mehr oder weniger Outside Money bereitstellt.
Viertens ist von elementarer Bedeutung, dass die (auf Reverse-Skew-Märkten) empirisch regelmäßig zu beobachtende antizyklische Entwicklung des Kurses, genauer: der Rendite eines Basiswertes und dessen impliziter Volatilität (vgl. dazu Delta, Ziff. 4) aus konzeptionellen Gründen in einem Volatility Skew sichtbar werden muss; vgl. hierzu ausführlich Volatility Surface, Ziff. 3, für einen innovativen Erklärungsansatz dieser Antizyklik unter Berücksichtigung von marktphasenabhängigen Kursänderungserwartungen, um gleichzeitig konsistent zu erklären,
- warum sich bei einer ausnahmsweise vorliegenden prozyklischen Entwicklung von Underlying und impliziter Volatilität keinerlei Tendenz zu einer "Entspannung" des Skew erkennen lässt,
- warum sich auch auf den (symmetrischen) Devisenmärkten vorübergehend ein Volatility Skew herausbilden kann (durch ausgeprägte situative Kursänderungserwartungen; vgl. auch Risk Reversal) und
- warum es überhaupt zu empirisch zu beobachtenden "Dellen" im Skew und einem Wiederanstieg im Bereich der Out-of-the-Money-Calls kommen kann; vgl. hierzu genauer Volatility Smirk.
3. Zum Forward Vertical Skew: Dieses entgegengerichtete Skew-Phänomen ist regelmäßig bei Optionen in Commodity-Märkten zu beobachten.
Unabhängig von Spezifika der Zusammenhänge für verschiedene Rohstoffe lässt sich verallgemeinern, dass – außer in der sehr langen Frist – eine persistente, inhärente Nachfrage einem in Relation dazu schwankenden Angebot gegenübersteht. Durch diese Nachfrage entsteht gleichsam eine natürliche Untergrenze der Preise, d.h. der dazugehörigen Futures-Kurse; umgekehrt können durch Missernten, Streiks und sonstige politische Risiken in den Erzeugerländern enorme "Preisexplosionen" verursacht werden. Die Absicherung gegen diese Beschaffungspreisrisiken ist strukturell upside orientiert und favorisiert im Unterschied zu Ziff. 2 den Erwerb von Out-of-the-Money-Calls. Ebenso ist in Umkehrung der o.g. Antizyklik vor allem bei agrarischen Rohstoffen regelmäßig eine prozyklische Entwicklung der Futures-Kurse eines Basiswertes und dessen impliziter Volatilität zu beobachten. Bei vielen mineralischen Rohstoffen (und Baumwolle) sowie nicht-metallischen Industrierohstoffen (z.B. Bauholz, Zellstoff) sind diese asymmetrischen Effekte wegen ihrer besseren Lager-(außer Elektrizität) und Transportfähigkeit, vor allem bei Edelmetallen, und/oder eines besser kontrollierbaren Angebots (z.B. aus Ölschiefer, Ölsanden) weniger stark ausgeprägt. Sobald sich ein Preistrend in den Augen der Marktteilnehmer etabliert hat, kommt es zu einem Anstieg der impliziten Volatilität, wie besonders deutlich am Rohölmarkt abgelesen werden kann.
4. Zum Forward und Reverse Horizontal Skew: Grundätzlich bildet der Volatility Cone den Rahmen, in dem sich ein spezifischer Horizontal Skew zu einem bestimmten Zeitpunkt und nach den verschiedenen Optionsserien unterschiedlich herausbildet.
a) Zur Zeitabhängigkeit des Horizontal Skew: Grundsätzlich sind Forward Skews häufiger anzutreffen als Reverse Skews und flacher als diese. Deshalb werden Forward Skews als "normal" angesehen, während eine Invertierung der zeitlichen Volatilitätsstruktur zwar häufiger vorkommt als bei der Zinsstruktur, aber dennoch als Ausnahme gilt. Tatsächlich ist davon auszugehen, dass es gegen Ende der Laufzeit auf einem eher hohen Volatilitätsniveau zu "nervösen" Gamma-Eindeckungen von At- und Near-the-Money-Stillhaltern kommt, insbesondere "gescheiterter" Gamma-Scalper (Volatilitätsstrategien, Ziff. 3. a) und solcher Stillhalter, die es durch Kursbewegungen im Basiswert in diesen Basispreisbereich (Moneyness) "verschlagen" hat. Inhaltlich ist die Sorge um ein solches "kurzes Gamma am kurzen Ende" auch theoretisch gerechtfertigt: Der Fair Value von Optionen mit kurzer Restlaufzeit wird durch das Black-Scholes-Modell insoweit unterschätzt, als auch kurzfristig noch mögliche Jumps (im Unterschied zur Black-Scholes-Diffusion) ins Geld oder aus dem Geld heraus oder abrupte Änderungen des Volatilitätsregimes (i.S. der modernen Regime-Switching-Modelle der Optionsbewertung) eintreten können; vor allem ergibt sich ein "flat peaked Gamma" around the Money. Dahingehende "Modellfehler" (vgl. implizite Volatilität, Ziff. 3) laufen naturgemäß in den impliziten Black-Scholes-Volatilitäten auf.
b) Zur Basispreisabhängigkeit des Horizontal Skew: Es bleibt zu klären, warum In-the-Money-Calls und Out-of-the-Money-Puts auf Reverse-Vertical-Skew-Märkten ceteris paribus im Contango stehen und sich Out-of-the-Money-Calls und In-the-Money-Puts eher in Backwardation befinden. Dieses Muster lässt sich abermals mit der antizyklischen oder prozyklischen Entwicklung des Kurses des Basiswertes und dessen impliziter Volatilität in Zusammenhang bringen: Wer auf niedrigem Volatilitätsniveau Volatilitätssteigerungen erwartet, muss konsistent mit Kursverlusten im Basiswert rechnen und wird im kurzen Laufzeitbereich Out-of-the-Money-(OTM-)Calls (und in zweiter Linie auch In-the-Money-(ITM-)Puts) wegen ihres niedrigeren (betragsmäßig höheren) Delta bevorzugen; ihr Preis wird also ansteigen, während ITM-Calls (und in zweiter Linie auch OTM-Puts) mit kurzer Restlaufzeit unattraktiv sind: Sollte sich die Volatilitätsprognose bewahrheiten, fällt diese Situation oft mit Kursrückgängen des Basiswertes zusammen, die bei In-the-Money-Calls mit kurzer Restlaufzeit sogar den erhofften Vega-Effekt überkompensieren können. Demgegenüber setzt sich am langen Ende der Vega-Effekt gegenüber diesem Vanna-Effekt (vgl. Skew-Risiko, Ziff. 3) durch, so dass Call- und Put-Preise gleicher (Delta-)Moneyness dort enger beieinander liegen. In Analogie zu den in der Literatur bereits bekannten Iota und Shadow Delta könnte man von einem "Vega-Iota", zusammengesetzt aus Vega und einem "Shadow Vega", sprechen:
dC/dσ = ∂C/∂σ + (∂C/∂S) (∂S/∂σ)
mit ∂C/∂σ als Vega bei angenommenem konstanten Kurs des Basiswertes S, ∂C/∂S als Delta der Option und ∂S/∂σ als Veränderung des Kurses des Basiswerts bei einer Veränderung dessen impliziter Volatilität. Das Shadow Vega ist der Kehrwert des Shadow Delta, so dass die unerwünschte Nebenwirkung der Shadow-Komponente, die beim Shadow Delta eher die beschriebenen Vanna-long-Positionen (OTM-Calls und ITM-Puts long; analog OTM-Puts und ITM-Calls short) desavouiert, ins Gegenteil umschlägt. Dass sich dies am langen Ende relativiert, hängt mit dem dort niedrigeren Vanna bei gleichzeitig höherem Vega zusammen. Die einschlägigen Sensitivitätskennzahlen Veta (positive Abhängigkeit des Vega von der Restlaufzeit) und Vatta (negative Abhängigkeit des Vanna von der Restlauzeit) erlauben, ein mit längerer Restlaufzeit ansteigendes Vega gegen ein mit längerer Restlaufzeit abfallendes Vanna vor allem intermediate, d.h. im mittleren Laufzeitenbereich, zu handeln.
Im Umkehrschluss wäre auf hohem Volatilitätsniveau auf den ersten Blick exakt die entgegengesetzte Konstellation zu erwarten, jedoch sind die Volatilität und die Korrelation von Volatilität und Kurs des Underlying positiv miteinander korreliert, d.h. in unruhigen Märkten verlaufen Volatilität und Kurs des Underlying eher gleichläufig (Prozyklik) als in ruhigen Märkten; mit zunehmender Volatilität von einem niedrigen Ausgangsniveau aus steigt also das Shadow Vega von einem eher hohen negativen Wert über einen Wert von Null zu einem eher positiven Wert an, so dass sich in abermaliger Umkehrung der basispreisbezogenen Sensitivitäten erneut das ursprünglich zu erklärende Muster einstellt.
c) Unabhängig davon kann ein konkreter Horizontal Skew die unterschiedlichsten Formen annehmen, zumal auch erwartete kürzerfristig positive Autokorrelationen im Underlying eine Rolle spielen und auf höheren Volatilitätsniveaus sogar einen Horizonal Smile auslösen können; dabei wirkt die durch den Volatility Cone gesteckten Ober- und Untergrenzen gewissermaßen als Widerstands- bzw. Unterstützungslinien.