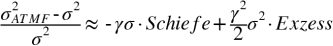Volatilitätsindex
Übersicht
zuletzt besuchte Definitionen...
1. Begriff: Index einer Terminbörse (z.B. Eurex, CBOE), der auf Basis der impliziten Volatilität von Optionen, die an dieser Terminbörse auf einen (Aktien-)Index gehandelt werden, berechnet wird. Ein Volatilitätsindex spiegelt im Grundsatz die durchschnittliche implizite Volatilität aller in den Index einbezogenen Optionen wider. So wurden seit 1994 an der Eurex Optionen auf den Deutschen Aktienindex (DAX) zur Ermittlung des VDAX und seit 2005 zusätzlich des VDAX-NEW herangezogen; mittlerweile hat der VDAX-NEW den VDAX ganz abgelöst, dessen Berechnung 2016 eingestellt wurde.
2. Konstruktion: Ein Volatilitätsindex soll die aktuell von den Marktteilnehmern für einen exakt festgelegten zukünftigen Zeitraum erwartete Volatilität des zugrunde gelegten (Aktien-)Index widerspiegeln; er lag für den VDAX bei 45 Tagen und wurde für den VDAX-NEW auf 30 Tage verkürzt. Im Unterschied zu gleichfalls zur Verfügung gestellten Subindizes, die die impliziten Volatilitäten für die unterschiedlichen Restlaufzeiten der aktuell an der Börse gehandelten Optionen abbilden, musste bzw. muss daher der Hauptindex mittels Interpolation aus zwei benachbarten Subindizes, die die Restlaufzeit von 45 bzw. 30 Tagen umschließen, konstruiert werden. Traditionelle Volatilitätsindizes wie bspw. der VDAX unterscheiden sich von modernen Volatilitätsindizes wie bspw. dem VDAX-NEW oder dem VSTOXX (auf den EURO STOXX 50) dadurch, dass zur Berechnung ausschließlich auf die besonders liquiden und als informationsträchtig geltenden At-the-Money-Optionen (ATMF; vgl. Moneyness) zurückgegriffen wird. Bei den modernen Volatilitätsindizes wird hingegen ein spezielles Optionsportfolio herangezogen, in dem Optionspositionen in ATMF-Optionen und Out-of-the-Money-Optionen derart gewichtet sind, dass der Wert des Portfolios gegen Kursschwankungen des Basiswertes neutralisiert ist und nur noch auf Volatilitätsveränderungen reagiert; vgl. genauer VDAX-NEW. Auf dieser Grundlage lässt sich zeigen, dass z.B. der VDAX-NEW im Kern die Quadratwurzel der arbitragefreien Swap-Rate eines synthetischen Varianzswaps mit einer dem Index entsprechenden Laufzeit abbildet. Der VDAX hingegen zeigte approximativ die arbitragefreie Swap-Rate eines synthetischen Volatilitätsswaps an; dies wurde indes erst 2005 von Carr/Lee erkannt und nachgewiesen.
3. Die Aufwärtsverzerrung der impliziten Volatilität: Ein besonders prägnantes stilisiertes Faktum der impliziten Volatilität, das sich vor allem für Volatilitätsindizes zeigt, ist deren systematische Aufwärtsverzerrung, und zwar sowohl gegenüber der heutigen tatsächlichen Volatilität, gemessen an einer kurzfristigen historischen Volatilität, dem sog. Volatility Spread (s.d., Ziff. 3), als auch gegenüber der zukünftigen tatsächlichen, also der realisierten Volatilität des Underlying; in empirischen Arbeiten sind seit dem 1987er Börsen-Crash Werte von über 20 Prozent als "normal" identifiziert worden. Dies ist auf verschiedene Einflüsse zurückzuführen, über deren relative Bedeutung bis heute noch kein abschließendes Urteil gefällt werden kann:
a) Konvexität bzw. Kurtosis (vgl. Skew-Risiko, Ziff. 2): Wie zu Varianz- und Volatilitätsswaps dargestellt, beinhaltet der Preis eines Varianzswaps immer auch einen Aufschlag für die Konvexitätseigenschaft der Varianz, der im Preis eines Volatilitätsswaps nicht enthalten ist. Deshalb musste der VDAX-NEW auch grundsätzlich höher notieren als der VDAX. Inhaltlich dafür verantwortlich ist unmittelbar die Volatilität der Volatilität ("Vola-Vola"), die wiederum implizit aus dem Strike von Varianzswaps oder dem Stand moderner Volatilitätsindizes im Vergleich zur (impliziten) ATMF-Volatilität (i.d.R. hälftig aus Puts und Calls) gewonnen werden kann. In empirischen Untersuchungen wird dieser – bisweilen als "Konvexitätsfehler" eingeordnete – Effekt in beachtlicher Einmütigkeit mit durchschittlich sechs bis sieben Prozent (oder ein bis zwei Vola-Punkten) angegeben; dabei ist der Schwankungsbereich mit ungefähr 2 Prozent bis 10 Prozent allerdings sehr hoch, jedenfalls gemessen an der Volatilität der realisierten "Vola-Vola", so dass andere Faktoren bereits auf dieser Ebene vermutet werden müssen.
b) Volatility Skew: Durch die replikations- und hedginggetriebene Bezugnahme moderner und (nach Carr/Lee auch) traditioneller Volatilitätsindizes auf den Volatility Skew spiegeln sich auch sämtliche Einflussfaktoren, die dessen Gestalt ausprägen, nicht zuletzt die i.d.R. negative Korrelation der Rendite des Index und dessen impliziter Volatilität (vgl. dazu Delta, Ziff. 4), in einer Verzerrung des Standes der Volatilitätsindizes gegenüber der tatsächlichen Volatilität wider, d.h. bei den hier relevanten Reverse Skews eben in einer Aufwärtsverzerrung. Dieser Effekt lässt sich bedauerlicherweise nicht wie unter a) durch beobachtbare Preisdifferenzen abgrenzen, sondern nur gemeinsam mit dem folgenden Faktor.
c) Volatilitätsrisikoprämien: (Vgl. Volatilitätsstrategien, Ziff. 4.a)). Der Stand traditioneller und moderner Volatilitätsindizes sollte bei Risikoaversion der Marktteilnehmer grundsätzlich eine Prämie für die von den Stillhaltern übernommenen Volatilitätsrisiken i.w.S. (einschließlich Skew-, Kurtosis-, an dieser Stelle aber ohne Korrelationsrisiken) enthalten. Diese lässt sich anhand der empirisch feststellbaren Aufschläge der impliziten ATMF-Volatilität gegenüber der heutigen und der zukünftigen tatsächlichen Volatilität erheben; hinzu kommt noch der jeweilige Einfluss schwankender Volatilitätsrisikoprämien (vgl. Volatilitätsstrategien, Ziff. 4.d), der sich nach derzeitigem Kenntnisstand aber nicht systematisch in einem Spread niederschlagen sollte. Die Investmentbank JPMorgan geht von einem Gesamteffekt von 2-3 Vola-Punkten aus.
d) Der Gesamtzusammenhang der unter a), b) und c) skizzierten Gründe für die Aufwärtsverzerrung der impliziten Varianz konnte auf theoretischer Basis sogar quantifiziert werden (Bakshi/Madan 2006), wobei der Fokus der Rechenbarkeit halber auf die tatsächliche Schiefe und Wölbung der Wahrscheinlichkeitsverteilung (Verteilungsfunktion) der Indexrendite gelegt wird:
mit dem zu erklärenden relativen, d.h. auf die tatsächliche Varianz σ2 normierten, Varianz-Spread, einem Parameter γ, der die gerade herrschende Risikoaversion abbildet, und dem Exzess, der als "Wölbung - 3" definiert ist (vgl. Portfolio-Theorie, Modellkritik, Ziff. 1.b). Dabei sind Schiefe und Exzess/Wölbung als dahingehende Erwartungen "des Marktes", mithin erneut implizite Größen, zu interpretieren, denen proprietäre Meinungen gegenübergestellt werden können – und von den Market Makern in Erfüllung ihrer Aufgabe gegenübergestellt werden müssen; für eine darin angelegte Self-Fulfilling Prophecy (technische Analyse) vgl. Volatility Surface, Ziff. 3). Unterschiede zwischen den impliziten Risikoaversionen verschiedener Basiswerte deuten auf die Möglichkeit einer Ausarbitrierung von durch erfolgreiches Finanzmarketing geschaffenen Loyalitätseffekten hin, wenn die Loyalität gefährdet erscheint. Es ist aufschlussreich, dass an dieser Stelle überhaupt kein Volatilitätsrisiko i.e.S. erscheint: Es geht vollständig in den höheren Momenten auf, womit Erkenntnisse aus dem Vanna-Volga Pricing (Skew-Risiko, Ziff. 3), bestätigt werden. Empirische Untersuchungen haben ergeben, dass der Einfluss der Schiefe, gemessen an den partiellen impliziten Risikoaversionen, als ungefähr doppelt so hoch eingeschätzt werden kann wie der der Wölbung; dabei nimmt erwartungsgemäß die relative Bedeutung der Wölbung mit längeren Laufzeiten zu. Raum gegeben ist jedenfalls auch der Modellierung einer konditionierten Bewertung (vgl. Faktormodelle, Ziff. 5) im Sinne schwankender Risikoprämien, die durch Endogenisierung des Risikoparameters bewerkstelligt werden müsste. Hinweise in diese Richtung vermittelt bereits die unter a) angesprochene empirische Überschuss-Volatilität der impliziten "Vola-Vola", vor allem in den USA; dort scheint die Angst speziell vor großen Verlusten im Sinne eines sog. Left-Tail-Risikos hiernach messbar stärker ausgeprägt zu sein als in Europa. Weiteren Aufschluss über die Zusammenhänge liefert ein weiterer moderner Volatilitätsindex: der seit 2015 von STOXX Ltd. veröffentlichte EURO STOXX 50 Volatility of Volatility Index (V-VSTOXX), in dem die implizite Volatilität von VSTOXX-Future-Optionen an der Eurex erfasst wird.
e) Hedgerisiken und Wettbewerbseffekte (vgl. Volatility Smile): Auch professionelle Stillhalter werden Volatilitätsrisikoprämien für ihre Hedgerisiken als "Speed-, Vanna- und Volga-Prämien" einfordern. Hier könnte der "technische Fortschritt" in den Hedgingprozessen i.V.m. Wettbewerbseffekten, auch zwischen den Market Makern, die gewisse Tendenz zu rückläufigen Volatility Spreads im Zeitablauf nachfrageseitig erklären. Auf der Angebotsseite kann generell ein zunehmender Wettbewerb im "Versicherungsmarkt" der impliziten Volatilität – als "Währung", in der die Versicherungsbeiträge entrichtet werden – Ähnliches bewirken; der regulierungsbedingte Abbau der gerade auf diesem Feld als überaus lukrativ geltenden Proprietory Desks der Investmentbanken spricht dagegen. Gewisse Markttransparenz ist jedenfalls durch einen speziellen Volatilitätsindex geschaffen worden: dem Variance Premium Trading Index, der von der Allianz-Tochtergesellschaft risklab berechnet wird; eine durchschnittliche jährliche Index-Rendite vom 1.1.2000 bis zum 31.5.2016 von 6,19 Prozent (bei einer Volatilität von 5,08 Prozent und einem maximalen Drawdown von 17,90 Prozent) verdeutlicht die Größenordnungen.
f) Volatilitätsänderungserwartungen: Nach der Erwartungstheorie der horizontalen Volatilitätsstruktur (vgl. Volatility Cone, Ziff. 2) und darauf basierender Volatilitätsstrategien (s.d., Ziff. 4.c)) ist nachvollziehbar, dass der relative Volatility Spread negativ mit dem Volatilitätsniveau korreliert ist, also mit steigender Volatilität erkennbar abnimmt und ungefähr ab Volatilitätsniveaus von 50 Prozent sogar negativ wird. Dies kann namentlich den in d) geschilderten Zusammenhang, vor allem die übliche positive Korrelation von Volatilitätsniveau und "Vola-Vola", überlagern.
g) Basiswert: Volatilitätsindizes fußen regelmäßig nicht auf (Einzel-)Aktienoptionen, sondern auf Aktienindex-Optionen. Damit sind die dort abgebildeten impliziten Volatilitäten bereits konstruktionsbedingt höher als die impliziten Volatilitäten der Indexmitglieder, und zwar aus zwei Gründen: Zum einen werden die strukturellen Downside-Absicherungsbedarfe auf Wertpapiermärkten sowohl gegen das Kursrisiko (vgl. Volatility Skew, Ziff. 2) als auch gegen das Korrelationsrisiko (vgl. Diversifikation, Ziff. 4) eher in Indexprodukten befriedigt, wodurch trotz Dispersion Trading ein latenter Correlation Spread zwischen impliziter und tatsächlicher Korrelation der Kurse der Indexmitglieder (vgl. Volatilitätsstrategien, Ziff. 3.e)) im Volatility Spread von Volatilitätsindizes aufläuft und ihn weiter nährt; so kann auch bei völlig unveränderten impliziten Volatilitäten auf Einzeltitelebene die implizite Volatilität auf Indexebene zunehmen, wenn die Marktteilnehmer – zu Recht – davon ausgehen, dass die Korrelationen der Einzeltitel in stärkeren Abschwungphasen zunehmen, diese aber länger auf sich warten lassen als befürchtet (so dass die tatsächliche Korrelation auf niedrigerem Niveau verharrt). Ein zweiter VDAX-NEW aus den wie beim DAX gewichteten impliziten Volatilitäten der Optionen auf die Aktien der Indexmitglieder könnte hier Abhilfe schaffen – und Geschäftsmöglichkeiten der Stillhalter beschneiden. Zum anderen werden die DAX-Optionen grundsätzlich im DAX-Future gehedgt, wodurch sich die höhere Volatilität des DAX-Future im Vergleich zum DAX auch im VDAX-NEW (wie bereits im VDAX) und damit in einem Volatility Spread gegenüber der tatsächlichen DAX-Volatilität niederschlägt; die höhere Volatilität ergibt sich aus dem sog. No-Arbitrage-Window, die der Index-Arbitrage Grenzen setzt. Auch hier könnte Abhilfe geschaffen werden, indem der VDAX nicht aus DAX-Optionen sondern aus DAX-Future-Optionen konstruiert würde; die Early-Exercise-Problematik (vgl. Volatility Smirk, Ziff. 4) sollte bei den hier relevanten At- und Out-of-the-Money-Index-Optionen kein Gegenargument sein.
4. Volatilität als Assetklasse? In ihrem Produktflyer zum VDAX-NEW äußert sich die Deutsche Börse AG sehr deutlich: "Die Volatilität eines Marktes ist mit der Wertentwicklung dieses Marktes negativ korreliert, so dass die reine Volatilität eine ideale Beimischung zur Diversifizierung von Portfolios ist – für institutionelle und private Anleger. Mit VDAX-NEW® haben die Deutsche Börse und Goldman Sachs eine transparente und nachbildbare Grundlage für Investments in reine Volatilität geschaffen. ... Volatilität ist damit für Anleger als separate Assetklasse handelbar." Das ist leider nicht zutreffend: Zum einen ist der VDAX-NEW keineswegs ohne weiteres handelbar, da er eben nicht die Varianz-Swap-Rate, sondern deren Quadratwurzel abbildet. Dies ist nicht trivial, sondern es ist gezeigt worden, dass es für die Replikation mittels Varianzswaps einer hochkomplexen dynamischen Handelsstrategie auf der Grundlage der impliziten Zeitstruktur der zukünftigen Varianz unter rigiden Modellannahmen bedarf, die sogar noch anspruchsvoller ist als die Replikation des VDAX. Eine naheliegende Replikation mittels des dazugehörigen Volatilitäts-Futures ist seit der Handelseinstellung des VDAX-NEW-Futures zum 1. Juli 2009 (vgl. Volatilitätsstrategien, Ziff. 5) überhaupt nicht mehr möglich und hätte ohnehin nur außerhalb eines Arbitragebandes (approximativ zwischen der impliziten Volatilität von Forward Start ATMF-Straddles als Untergrenze und der Quadratwurzel der forward-starting Varianz-Swap-Rate als Obergrenze) basisrisikofrei funktioniert. Zum anderen erfüllt die Long-Position in impliziter Volatilität zwar die Anforderungen an eine Assetklasse nach Sharpe, allerdings rechtfertigt selbst das empirisch feststellbare Beta (theoretischer Varianzswaps) von -3 bis -4 nicht eine negative Rendite in den empirisch feststellbaren Größenordnungen: Die Diversifikationsvorteile werden nach herkömmlicher Lesart schlicht zu teuer eingekauft, d.h. die Beimischung von Volatilitätsinstrumenten verringert zwar tatsächlich das Portefeuille-Risiko, aber auch die erwartete Portefeuille-Rendite, und zwar über Gebühr. Genau umgekehrt ist es vielmehr die Short-Position in impliziter Volatilität, ggf. rolling mit Kurzläufern, und damit letztlich die Volatilitätsrisikoprämie, die als attraktive Assetklasse identifiziert werden kann. Als Rentensurrogat tritt sie vor allem in Niedrigzinsphasen in direkte Konkurrenz zur festverzinslichen Anlage (auch in Corporate Bonds) und umso mehr zu Riding-the-Yield-Kurve-Strategien mit Langläufern: Das laufend generierte Theta bzw. die laufend vereinnahmten Volatilitätsprämien auf das "Versicherungskapital" nehmen die Rolle von Coupons ein, eine Break-even-Volatilitätsstrukturkurve erlaubt die Risikoabschätzung für Volatilitätsanstiege in Analogie zur Break-even-Renditestrukurkurve im aktiven Bond-Portfoliomanagement und gibt Anhaltspunkte für ein Tail-Risk-Overlay. Als noch effizienter stellt sich die Kombination mit Leerverkäufen im Underlying dar, was durch die Antizyklizität von Kurs und impliziter Volatilität – nun auf beiden Seiten mit negativen Vorzeichen wirksam – i.V.m. einem Geldmarktinstrument in ein vergleichbar risikoarmes Investment einmündet; entsprechende Anteile an Hedge Funds sind auf dem Markt erhältlich, und die Kommunikationspolitik in Sachen "Long Volatility als Assetklasse" befürsorgt die Marktgegenseite.
5. Zur Volatilitätsprognose mit Volatilitätsindizes (vgl. grundlegend die Ausführungen zur impliziten Volatilität, Ziff. 4): Es hat sich erwiesen, dass der VDAX-NEW erwartungsgemäß zwar eine hochgradig verzerrte Prognose der zukünftigen tatsächlichen Volatilität liefert, die aber durchaus als supereffizient i.S. der Theorie der optimalen Versuchsplanung bezeichnet werden kann: Der mittlere quadratische Fehler ist deutlich geringer als beim VDAX, d.h. der VDAX-NEW liefert ungenauere Prognosen, die dafür aber informativer sind; bei der Volatilitätsprognose ist lediglich ein historischer Durchschnitt der Aufwärtsverzerrung (inkl. "Konvexitätsfehler") in Abzug zu bringen, der sich in einer Größenordnung von 3-4 Vola-Punkten bewegt. Inhaltlich geht dies darauf zurück, dass eine ATMF-Volatilität wie beim VDAX die Marktmeinung über die zukünftige tatsächliche Volatilität lediglich bei einem unveränderten Markt widerspiegelt, während der VDAX-NEW qua Anbindung an den Volatility Skew diese Marktmeinung unabhängig von Marktbewegungen und damit auch Crash-Szenarien abbildet; die Verkürzung des zu prognostizierenden Zeitraums von 45 auf 30 Tage tut ihr Übriges. Wie beschrieben, leidet die Prognoseeigenschaft des VDAX-NEW (wie auch des DAX) gleichwohl an hier sachfremdem Noise durch den Einfluss der (ggf. auch schwankenden) Volatilitätsrisikoprämien. Insoweit erscheint es sinnvoller, anstelle des gesamten Volatility Skew auf eine singuläre, die sog. korrelationsimmune Volatilität, zu rekurrieren: Diese findet sich im Basispreispreis eines Shadow Delta, inhaltlich eines Shadow Vega (vgl. Volatility Skew, Ziff. 4.b), von null; so dürfte die unmittelbare Anbindung an die geboten erscheinende Modellierung einer konditionierten Bewertung des Risikos schwankender Risikoprämien (vgl. Faktormodelle, Ziff. 5) eher gedeihen.